Tak, ujednolicenie danych jest pożądane podczas uczenia się regresji procesów Gaussa. Istnieje wiele powodów:

1. W typowym modelu regresji procesów Gaussa zakładamy, że wynik $ y $ ma zerową średnią, więc powinniśmy ustandaryzować $ y $, aby pasował do naszego założenia.
2. Dla wielu funkcji kowariancji mamy parametry skali w funkcjach kowariancji. Dlatego powinniśmy ustandaryzować dane wejściowe, aby uzyskać lepsze oszacowanie parametrów funkcji kowariancji.
3. Regresja procesów Gaussa jest podatna na problemy numeryczne, ponieważ musimy odwrócić źle uwarunkowaną macierz kowariancji. Aby zmniejszyć ten problem, powinieneś ustandaryzować swoje dane.

Niektóre pakiety wykonują tę pracę za Ciebie, na przykład GPR w sklearn ma opcję normalizuj dla normalizacji wejść, ale nie wyjść ( http://scikit-learn.org/stable/modules/generated/sklearn.gaussian_process.GaussianProcess.html)

Zgadzam się z odpowiedzią Aleksieja Zajcewa (i omówieniem tej odpowiedzi), że standaryzacja jest dobra do zrobienia z różnych powodów również na wynikach. Chciałbym jednak tylko dodać przykład, dlaczego standaryzacja wyników może być ważna.

Przykładem, w którym normalizacja / standaryzacja wyjścia jest ważna, to małe i zaszumione wartości wyjściowe. Poniższy rysunek ilustruje to na bardzo prostym przykładzie. Kod MATLABa poniżej rysunku.

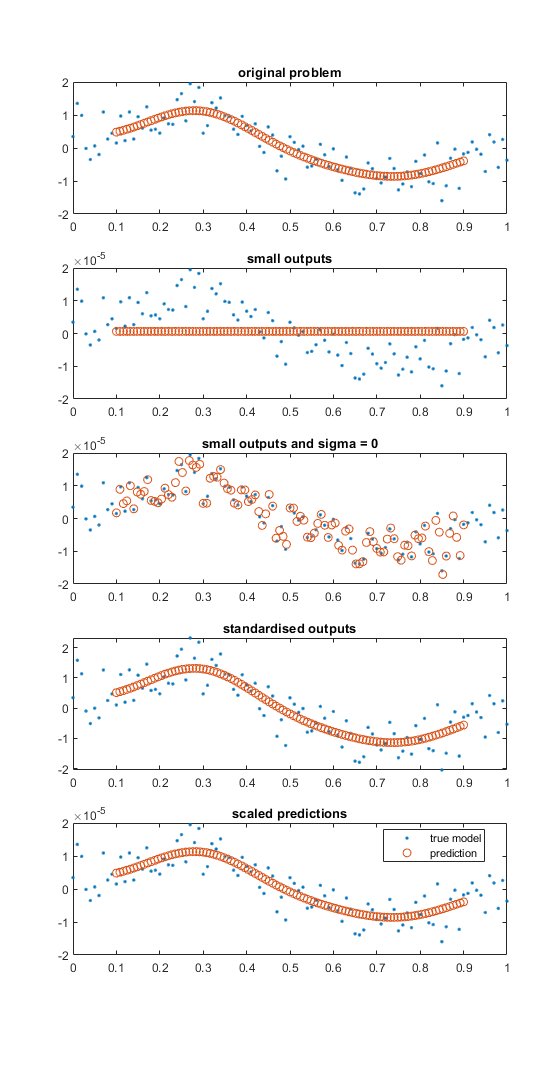
Niebieskie kropki reprezentują zaszumione próbki funkcji sin (). Pomarańczowe / czerwone kółka reprezentują przewidywane wartości procesu Gaussa.

1. W górnym dolnym wykresie amplituda jest równa jedności (z szumem).
2. W drugim wykresie pomocniczym wartości wyjściowe zostały przeskalowane za pomocą 1e-5 i widzimy, że model procesu Gaussa (z ustawieniami domyślnymi) przewiduje model stały. Domyślne ustawienia optymalizują parametr szumu i mają dość wysoką dolną granicę.
3. W trzecim wykresie pomocniczym parametr szumu jest ustawiony na zero i nie jest optymalizowany. W tym przypadku model zbyt mocno pasuje.
4. Czwarty wykres pomocniczy przedstawia standardowe wyniki i model dopasowany do tych danych.
5. W ostatnim wykresie podrzędnym wyniki są skalowane wstecz z operacji standaryzacji (nie skalowane z powrotem do wartości pierwotnych), a także wartości przewidywane są skalowane. Zwróć uwagę, że przewidywane wartości są skalowane przy użyciu średniej i odchylenia standardowego ze standaryzacji danych uczących.

 , funkcja valid_normgp ()
% małych wyników

% danych
x = 0: 0,01: 1; x = x (:);
xp = przestrzeń linowa (0,1, 0,9, długość (x)); xp = xp (:);

% modelu bez hałasu
y = sin (2 * pi * x) + 5e-1 * randn (length (x), 1);

% trenuje i przewiduje model GP
mdl = fitrgp (x, y);
yp = przewidzieć (mdl, xp);

postać
subplot (5, 1, 1)
plot (x, y, '.')
czekaj
plot (xp, yp, 'o')
tytuł ('oryginalny problem')

%% sprawia, że ​​wyjścia są małe (poniżej dolnej granicy szumu)
ym = y / 1e5;

% trenuje i przewiduje model GP
mdlm = fitrgp (x, ym);
ypm = przewidzieć (mdlm, xp (:));

subplot (5, 1, 2)
plot (x, ym, '.')
czekaj
plot (xp, ypm, „o”)
tytuł („małe produkty”)

%% wyświetla małe i ustawia sigma = 0

% trenuje i przewiduje model GP
mdlm1 = fitrgp (x, ym, 'Sigma', 1e-12, 'ConstantSigma', true, 'SigmaLowerBound', eps);
ypm1 = przewidzieć (mdlm1, xp (:));

subplot (5, 1, 3)
plot (x, ym, '.')
czekaj
plot (xp, ypm1, 'o')
tytuł ('małe wyniki i sigma = 0')

%% normalizuj / standaryzuj
nu = średnia (ym);
sigma = std (ym);
yms = (ym - nu) / sigma;

% trenuje i przewiduje model GP
mdlms = fitrgp (x, yms);
ypms = przewidzieć (mdlms, xp (:));

subplot (5, 1, 4)
plot (x, yms, '.')
czekaj
plot (xp, ypms, „o”)
tytuł ('standardowe wyjścia')

% rescale
ypms2 = ypms * sigma + nu;

subplot (5, 1, 5)
plot (x, ym, '.')
czekaj
plot (xp, ypms2, „o”)
tytuł („skalowane prognozy”)

legenda („prawdziwy model”, „prognoza”, „lokalizacja”, „najlepsza”)
koniec