Jedno z najprostszych rozwiązań uznaje, że zmiany między prawdopodobieństwami, które są małe (np. 0,1) lub których uzupełnienia są małe (np. 0,9), są zwykle bardziej znaczące i zasługują na większą wagę niż zmiany średnich prawdopodobieństw ( np. 0,5).

Na przykład zmiana z 0,1 na 0,2 (a) podwaja prawdopodobieństwo, podczas gdy (b) zmienia się prawdopodobieństwo komplementarne tylko o 1/9 (zmniejszając je z 1-0,1 = 0,9 do 1 -0,2 na 0,8), natomiast zmiana z 0,5 na 0,6 (a) zwiększa prawdopodobieństwo tylko o 20%, a (b) zmniejsza prawdopodobieństwo komplementarne tylko o 20%. W wielu zastosowaniach ta pierwsza zmiana jest, a przynajmniej powinna być, uważana za prawie dwukrotnie większą niż druga.

W każdej sytuacji, w której równie sensowne byłoby użycie prawdopodobieństwa (czegoś ) lub jej uzupełnienie (czyli prawdopodobieństwo, że coś się nie wydarzy), powinniśmy przestrzegać tej symetrii.

Te dwie idee - poszanowania symetrii między prawdopodobieństwami $ p $ a ich dopełnieniami $ 1- p $ i wyrażania zmian raczej względnie niż bezwzględnie - sugerują, że porównując dwa prawdopodobieństwa $ p $ i $ p '$ powinniśmy śledzić zarówno ich stosunki $ p' / p $, jak i ich uzupełnienia $ ( 1-p) / (1-p ') $. Podczas śledzenia współczynników prostsze jest użycie logarytmów, które zamieniają je na różnice. Ergo, dobrym sposobem na wyrażenie prawdopodobieństwa $ p $ w tym celu jest użycie $$ z = \ log p - \ log (1-p), $$, które jest znane jako zaloguj kursy lub logit $ p $. Dopasowane kursy logarytmiczne $ z $ można zawsze zamienić z powrotem na prawdopodobieństwa, odwracając logit; $$ p = \ exp (z) / (1+ \ exp (z)). $$ Ostatnia linia poniższego kodu pokazuje, jak to się robi.

To rozumowanie jest raczej ogólne: prowadzi do dobrej domyślnej procedury wstępnej do badania dowolnego zestawu danych obejmującego prawdopodobieństwa. (Dostępne są lepsze metody, takie jak regresja Poissona, gdy prawdopodobieństwa są oparte na obserwacji stosunków „sukcesów” do liczby „prób”, ponieważ prawdopodobieństwa oparte na większej liczbie prób zostały zmierzone w bardziej wiarygodny sposób. Nie wydaje się to być w tym przypadku, gdzie prawdopodobieństwa są oparte na uzyskanych informacjach. Można przybliżyć metodę regresji Poissona przy użyciu ważonych najmniejszych kwadratów w poniższym przykładzie, aby uwzględnić dane, które są mniej lub bardziej wiarygodne.)

Spójrzmy na przykład.

Wykres rozrzutu po lewej stronie przedstawia zbiór danych (podobny do tego w pytaniu) wykreślony w postaci log kursów. Czerwona linia to zwykłe dopasowanie metodą najmniejszych kwadratów. Ma niskie R ^ 2 $, co wskazuje na duże rozproszenie i silną „regresję do średniej”: linia regresji ma mniejsze nachylenie niż główna oś tej eliptycznej chmury punktów. To znajome ustawienie; łatwo go zinterpretować i przeanalizować za pomocą funkcji lm R lub jej odpowiednika.

Wykres rozrzutu po prawej stronie przedstawia dane w kategoriach prawdopodobieństwa , tak jak zostały pierwotnie nagrane. Wykreślane jest to samo dopasowanie: teraz wygląda na zakrzywione ze względu na nieliniowy sposób, w jaki dziennik prawdopodobieństwa jest konwertowany na prawdopodobieństwa.

W sensie błędu średniej kwadratowej em> pod względem log kursów ta krzywa jest najlepiej dopasowana.

Nawiasem mówiąc, w przybliżeniu eliptyczny kształt chmury po lewej stronie i sposób, w jaki śledzi ona linię najmniejszych kwadratów, sugeruje, że model regresji najmniejszych kwadratów jest rozsądny: dane można odpowiednio opisać za pomocą zależności liniowej - podana stosowane są kursy logarytmiczne - a odchylenie pionowe wokół linii jest mniej więcej tej samej wielkości, niezależnie od położenia poziomego (homoskedastyczność). (W środku znajdują się niezwykle niskie wartości, które mogą zasługiwać na dokładniejsze zbadanie). Oceń to bardziej szczegółowo, wykonując poniższy kod za pomocą polecenia plot (fit) , aby zobaczyć standardową diagnostykę. Już samo to jest mocnym powodem, aby analizować te dane zamiast prawdopodobieństw za pomocą dzienników kursów.

  ## Odczytaj dane z tabeli z (X, Y) = (X, prawdopodobieństwo) par. # x <- read.table ("F: /temp/data.csv", sep = ",", col.names = c ("X", " Y ")) ## Zdefiniuj funkcje do konwersji między prawdopodobieństwami` p` i logami kursów `z`. # (Gdy niektóre prawdopodobieństwa faktycznie są równe 0 lub 1, niewielka korekta - określona przez dodatnią # wartość` e`-- należy zastosować, aby uniknąć nieskończonych logarytmicznych kursów.) # logit <- function (p, e = 0) {x <- (p-1/2) * (1-e) + 1/2; log (x) - log (1-x)} logistyczna funkcja < (z, e = 0) {y <- exp (z) / (1 + exp (z)); (y-1/2) / (1-e) + 1/2} ## Dopasuj dziennik kursów używając najmniejszych kwadratów. # b <- coef (fit <- lm (logit (x $ Y) ~ x $ X) ) ## Wykreśl wyniki na dwa sposoby. # Par (mfrow = c (1,2)) plot (x $ X, logit (x $ Y), cex = 0,5, col = "Gray", main = "Least Squares Fit ", xlab =" X ", ylab =" Log odds ") abline (b, col =" Red ", lwd = 2) plot (x $ X, x $ Y, cex = 0,5, col =" Gray ", main = "LS Fit Re-expression", xlab = "X", ylab = "Probability") krzywa (logistic (b [1] + b [2] * x), col = "Red", lwd = 2, add = TRUE)  

Biorąc pod uwagę wypaczenie danych z x, oczywistą pierwszą rzeczą do zrobienia jest użycie regresji logistycznej ( link wiki). Więc jestem z Whuberem w tej sprawie. Powiem, że samo $ x $ będzie miało duże znaczenie, ale nie wyjaśni większości odchyleń (odpowiednika całkowitej sumy kwadratów w OLS). Można więc zasugerować, że istnieje inna zmienna towarzysząca oprócz $ x $, która pomaga w wyjaśnianiu (np. Osoby dokonujące klasyfikacji lub zastosowaną metodę), Twoje dane $ y $ są już [0,1]: czy wiesz, czy oni reprezentują prawdopodobieństwa lub wskaźniki występowania? Jeśli tak, powinieneś wypróbować regresję logistyczną, używając nieprzekształconych $ y $ (zanim będą to współczynniki / prawdopodobieństwa).

Obserwacja Petera Floma ma sens tylko wtedy, gdy twoja y nie jest prawdopodobieństwem. Sprawdź plot (density (y)); rug (y) w różnych segmentach $ x $ i zobacz, czy widzisz zmieniającą się dystrybucję Beta lub po prostu uruchom betareg . Zauważ, że dystrybucja beta jest również wykładniczą dystrybucją rodzinną i dlatego powinno być możliwe modelowanie jej za pomocą glm w R.

Aby dać ci wyobrażenie o tym, co mam na myśli przez logistykę regresja:

  # `` rzeczywista '' zależność, w której y jest interpretowane jako prawdopodobieństwo sukcesuy = runif (400) x = -2 * (log (y / (1-y)) - 2 ) + rnorm (400, sd = 2) glm.logit = glm (y ~ x, rodzina = dwumian); wykres podsumowujący (glm.logit) (y ~ x); wymagają (daleko); grid () points (x, ilogit (coef (glm.logit)% *% rbind (1.0, x)), col = "red") tt = runif (400) # przykład twojej nietransformowanej regresjinewy = ifelse (tt < y, 1, 0) glm.logit = glm (nowość ~ x, rodzina = dwumian); podsumowanie (glm.logit) # jeśli nie ma dobrego dopasowania w prawdopodobieństwie ogona, wypróbuj inną funkcję łącza lub oversampling z korektą (będzie gorzej tutaj, ale może nie w twoich danych) glm.probit = glm (y ~ x, family = dwumian (link = probit)); podsumowanie (glm.probit) glm.cloglog = glm (y ~ x, rodzina = dwumian (link = cloglog)); podsumowanie (glm.cloglog)  

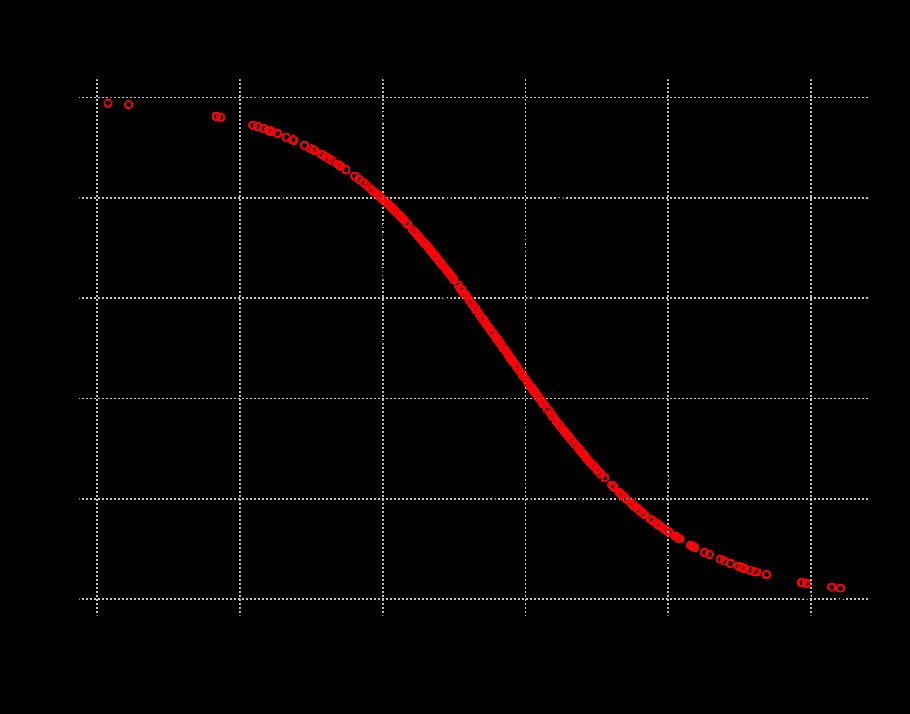
EDYCJA: po przeczytaniu komentarzy:

Biorąc pod uwagę, że „Wartości y to prawdopodobieństwa przynależności do określonej klasy, uzyskane z uśredniania klasyfikacji wykonanych ręcznie przez ludzi”, zdecydowanie zalecam wykonanie regresji logistycznej na podstawie danych podstawowych. Oto przykład:

Załóżmy, że patrzysz na prawdopodobieństwo, że ktoś zgodzi się na propozycję ($ y = 1 $ zgadzam się, $ y = 0 $ nie zgadzam się) z zachętą $ x $ między 0 a 10 (można przekształcić dziennik, np. wynagrodzenie). Dwie osoby proponują kandydatom ofertę („Jill and Jack”). Prawdziwy model jest taki, że kandydaci mają podstawowy wskaźnik akceptacji, który rośnie wraz ze wzrostem zachęty. Ale zależy to również od tego, kto składa ofertę (w tym przypadku mówimy, że Jill ma większe szanse niż Jack). Załóżmy, że łącznie pytają 1000 kandydatów i zbierają ich dane dotyczące akceptacji (1) lub odrzucenia (0).

  require (daleko) people = c ("Jill", "Jack") proposer = sample (people, 1000, replace = T) incentive = runif (1000, min = 0, max = 10) szum = rnorm (1000, sd = 2) # bazowe prawdopodobieństwo uzgodnienia wynosi około 12% (ilogit (-2)) agrees = ilogit (-2 + 1 * zachęta + ifelse (proposer == "Jill", 0, -0,75) + szum) tt = runif (1000) obserwowaneAgrees = ifelse (tt < zgadza się, 1,0) glm.logit = glm (zaobserwowaneAgrees ~ zachęta + proposer, rodzina = dwumian); podsumowanie (glm.logit) 

Z podsumowania widać, że model pasuje całkiem dobrze. Odchylenie to $ \ chi ^ 2_ {n-3} $ (standard z $ \ chi ^ 2 $ to $ \ sqrt {2.df} $). Co pasuje i bije model o ustalonym prawdopodobieństwie (różnica w odchyleniach wynosi kilkaset przy $ \ chi ^ 2_ {2} $). Trochę trudniej jest to narysować, biorąc pod uwagę, że istnieją tutaj dwie zmienne towarzyszące, ale masz pomysł.

  xs = coef (glm.logit)% *% rbind (1, incentive, as.factor (proposer)) ys = as.vector (unlist (ilogit (xs))) plot (ys ~ incentive, type = "n"); wymagają (daleko); grid () points (incentive [proposer == "Jill"], ys [proposer == "Jill"], col = "red") points (incentive [proposer == "Jack"], ys [proposer == "Jack "], col =" blue ")  

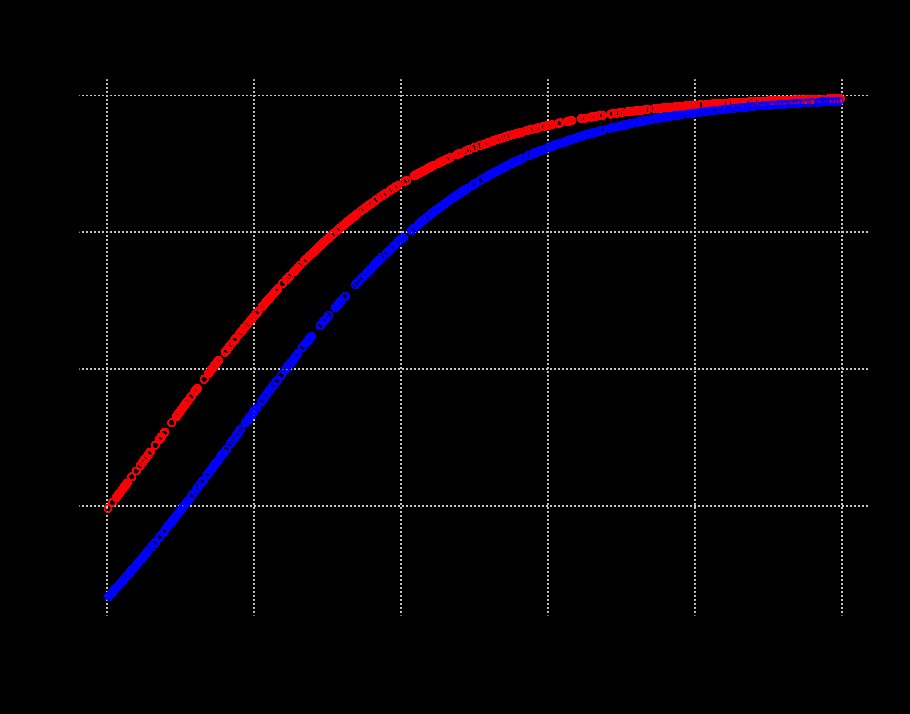
Jak widać, Jill ma łatwiejszy czas na uzyskanie dobrego współczynnika trafień niż Jack, ale to znika wraz ze wzrostem zachęty.

Zasadniczo powinieneś zastosować ten typ modelu do oryginalnych danych. Jeśli wynik jest binarny, zachowaj 1/0, jeśli jest wielomianowy, potrzebujesz wielomianowej regresji logistycznej. Jeśli uważasz, że dodatkowe źródło wariancji nie jest kolektorem danych, dodaj kolejny czynnik (lub zmienną ciągłą), cokolwiek uważasz, że ma sens dla twoich danych. Dane są jako pierwsze, drugie i trzecie, a dopiero potem do gry wchodzi model.

Model regresji liniowej nie jest dobrze dopasowany do danych. Można by się spodziewać, że regresja będzie wyglądała następująco:

ale zdając sobie sprawę z tego, co robi OLS, oczywiste jest, że to nie jest to, co otrzymasz. Graficzna interpretacja zwykłych najmniejszych kwadratów polega na tym, że minimalizuje do kwadratu pionową odległość między linią (hiperpłaszczyzną) a danymi. Oczywiście fioletowa linia, którą nałożyłem, ma kilka ogromnych reszt z $ x \ in (-7,4,5) $ i ponownie po drugiej stronie 3. Dlatego niebieska linia jest lepiej dopasowana niż fioletowa.

Ponieważ Y jest ograniczone przez 0 i 1, zwykła regresja metodą najmniejszych kwadratów nie jest odpowiednia. Możesz spróbować regresji beta. W R znajduje się pakiet betareg .

Spróbuj czegoś takiego

  install.packages ("betareg") biblioteka (betareg) betamod1 <- betareg (y ~ x, data = DATASETNAME)  

więcej informacji

EDYCJA: Jeśli chcesz uzyskać pełne omówienie regresji beta, jej zalet i wad, zobacz Lepszy wyciskacz do cytryn : Regresja największego prawdopodobieństwa ze zmiennymi zależnymi o rozkładzie beta autorstwa Smithsona i Verkuilena

Najpierw możesz chcieć dokładnie wiedzieć, co robi model liniowy. Próbuje zamodelować związek postaci

$$ Y_i = a + bX_i + \ epsilon_i $$

Gdzie $ \ epsilon_i $ spełnia określone warunki (heteroskedastyczność, jednorodna wariancja i niepodległość - wikipedia to dobry początek, jeśli to nie dzwoni). Ale nawet jeśli te warunki są sprawdzone, nie ma absolutnie żadnej gwarancji, że będzie to „najlepsze dopasowanie” w sensie, którego szukasz: OLS próbuje po prostu zminimalizować błąd w kierunku Y, co robi w Twoim ale który nie wydaje się być najlepszym rozwiązaniem.

Jeśli model liniowy jest naprawdę tym, czego szukasz, możesz spróbować trochę przekształcić zmienne, aby rzeczywiście można było dopasować OLS, lub po prostu wypróbuj zupełnie inny model. Możesz zajrzeć do PCA lub CCA lub jeśli naprawdę zależy Ci na modelu liniowym, wypróbuj rozwiązanie metodą najmniejszych kwadratów, które może zapewnić lepsze „dopasowanie”, ponieważ dopuszcza błędy w obu kierunkach.