Zwykle nie nazywałbyś wartości obserwowanej „wartością szacunkową”.

Jednak pomimo tego obserwowana wartość jest technicznie oszacowaniem średniej w jej poszczególnych $ x $, a potraktowanie jej jako oszacowania faktycznie powie nam sens, w którym OLS jest lepszy w szacowaniu średniej.

Ogólnie rzecz biorąc, regresja jest używana w sytuacji, gdy gdybyś pobrał inną próbkę z tymi samymi $ x $, nie uzyskałbyś takich samych wartości $ y $. W zwykłej regresji traktujemy $ x_i $ jako stałe / znane ilości, a odpowiedzi, $ Y_i $ jako zmienne losowe (z obserwowanymi wartościami oznaczonymi $ y_i $).

Używając bardziej powszechnego zapisu, piszemy

$$ Y_i = \ alpha + \ beta x_i + \ varepsilon_i $$

Pojęcie szumu $ \ varepsilon_i $ jest ważne, ponieważ obserwacje nie są prawidłowe na linii populacji (gdyby tak było, regresja nie byłaby potrzebna; dowolne dwa punkty dałyby linię populacji); model dla $ Y $ musi uwzględniać wartości, które przyjmuje, aw tym przypadku rozkład losowych błędów uwzględnia odchylenia od („prawdziwej”) linii.

Oszacowanie średniej w punkcie $ x_i $ dla zwykłej regresji liniowej ma wariancję

$$ \ Big (\ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum (x_i- \ bar {x}) ^ 2} \ Big) \, \ sigma ^ 2 $$

natomiast oszacowanie oparte na wartości obserwowanej ma wariancję $ \ sigma ^ 2 $.

Można pokazać, że dla $ n $ co najmniej 3, $ \, \ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum (x_i- \ bar {x}) ^ 2} $ wynosi nie więcej niż 1 (ale może być - aw praktyce zwykle jest - znacznie mniejsze). [Dalej, kiedy oszacujesz dopasowanie na $ x_i $ na $ y_i $, pozostaje Ci również kwestia, jak oszacować $ \ sigma $.]

Zamiast jednak kontynuować formalną demonstrację, zastanów się przykład, który, mam nadzieję, może być bardziej motywujący.

Niech $ v_f = \ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum ( x_i- \ bar {x}) ^ 2} $, współczynnik, przez który mnoży się wariancję obserwacji, aby otrzymać wariancję dopasowania na poziomie $ x_i $.

Jednak popracujmy nad skalą względnego błędu standardowego zamiast względnej wariancji (to znaczy, spójrzmy na pierwiastek kwadratowy z tej wielkości); przedziały ufności dla średniej w określonym $ x_i $ będą wielokrotnością $ \ sqrt {v_f} $.

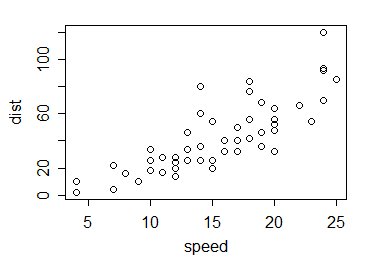
A więc do przykładu. Weźmy dane cars w R; to jest 50 obserwacji zebranych w latach dwudziestych XX wieku na temat prędkości samochodów i odległości potrzebnych do zatrzymania:

Jak więc obliczają się wartości $ \ sqrt {v_f} $ porównać z 1? W ten sposób:

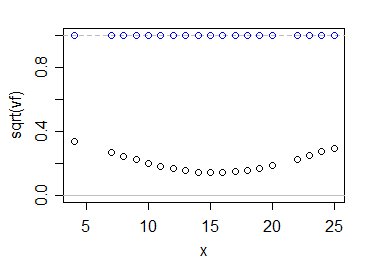
Niebieskie kółka pokazują wielokrotności $ \ sigma $ dla twojego oszacowania, podczas gdy czarne pokazują to dla zwykłego oszacowania najmniejszych kwadratów. Jak widać, wykorzystanie informacji ze wszystkich danych znacznie zmniejsza naszą niepewność co do tego, gdzie leży średnia populacji - przynajmniej w tym przypadku i oczywiście biorąc pod uwagę, że model liniowy jest poprawny.

W rezultacie , jeśli wykreślimy (powiedzmy) 95% przedział ufności dla średniej dla każdej wartości x $ (w tym w miejscach innych niż obserwacja), granice przedziału przy różnych $ x $ są zwykle małe w porównaniu z zmienność danych:

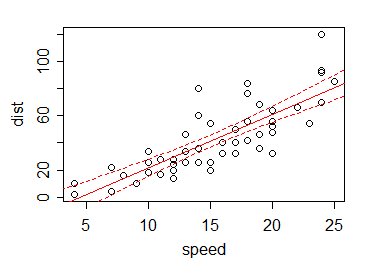
Jest to korzyść z „zapożyczenia” informacji z wartości danych innych niż bieżąca.

Rzeczywiście, możemy wykorzystać informacje z innych wartości - poprzez zależność liniową - aby uzyskać dobre oszacowania wartości w miejscach, w których nawet nie mamy danych. Weź pod uwagę, że w naszym przykładzie nie ma danych przy x = 5, 6 lub 21. Przy sugerowanym estymatorze nie mamy tam żadnych informacji - ale za pomocą linii regresji możemy nie tylko oszacować średnią w tych punktach (i przy 5,5 i 12,8 i tak dalej), możemy podać dla niej przedział - choć znowu taki, który opiera się na stosowności założeń liniowości (i stałej wariancji Y $ s i niezależności).

Po pierwsze, równanie regresji wygląda następująco:

\ begin {equation} Y_i = \ alpha + \ beta X_i + \ epsilon_i \ end {equation}

Występuje błąd , $ \ epsilon $. Jak się okazuje, ten błąd ma kluczowe znaczenie dla udzielenia odpowiedzi na Twoje pytanie. Jaki dokładnie jest termin błędu w Twojej aplikacji? Jedną z powszechnych interpretacji tego jest „wpływ wszystkiego innego niż $ X $, który wpływa na $ Y $”. Jeśli taka jest Twoja interpretacja terminu błędu, to $ Y_i $ jest najlepszą miarą tego, czym naprawdę jest $ Y_i $.

Z drugiej strony, w niektórych rzadkich przypadkach interpretujemy termin błędu jako wyłącznie błąd pomiaru --- błąd wywołany błędem operatora w używaniu przyrządu naukowego lub błąd wynikający z naturalnie ograniczonej precyzji przyrządu. W takim przypadku „rzeczywista” wartość $ Y_i $ to $ \ alpha + \ beta X_i $. W takim przypadku należy użyć prognozy OLS $ Y_i $ zamiast rzeczywistej wartości $ Y_i $, jeśli $ V (\ epsilon_i) >V (\ hat {\ alpha} _ {OLS} + \ hat {\ beta} _ {OLS} X_i) $ - to znaczy, jeśli wariancja błędu wynikająca z zastąpienia $ \ alpha $ i $ \ beta $ ich estymatorami OLS jest mniejsza niż wariancja błędu pomiaru.

Oryginalna wartość nie jest wartością szacunkową (z wyjątkiem faktu, że może mieć błąd pomiaru): jest to wartość Y dla określonego tematu (np. osoby lub czegokolwiek). Przewidywana wartość z równania to oszacowanie: jest to oszacowanie oczekiwanej wartości Y przy danej wartości X.

Zróbmy to konkretnie:

Powiedzmy, że Y to waga, a X to wzrost. Powiedzmy, że mierzysz i ważysz grupę ludzi. Powiedzmy, że Jill ma 5'0 i 105 funtów. To jest jej wzrost i waga. Równanie da ci inną przewidywaną wartość wagi dla osoby, która ma 5'0 ". To nie jest przewidywana wartość dla Jill - nie musisz przewidywać ani szacować jej wagi, znasz to z precyzją Jest to wartość przewidywana dla jakiejś „typowej osoby” o wartości 5'0.

Równanie powinno wyglądać tak: $$ \ nazwa operatora {E} (Y) = \ alpha + \ beta x $$; to jest oczekiwana wartość $ Y $ przy danej wartości $ x $. Tak więc, jeśli twój model & ma rację, wykonasz wystarczającą liczbę obserwacji Y $ przy tej wartości $ x $, to powie ci, jaka będzie średnia wartość $ Y $. Na dłuższą metę lepiej przewidujesz, używając tej średniej niż obserwowanej wartości.

Zazwyczaj OLS nie jest motywowany porównaniem szacowanej odpowiedzi $ \ hat {Y_i} $ z obserwowaną odpowiedzią $ Y_i $. Zamiast tego, jeśli otrzyma nowy zestaw wartości dla wartości predykcyjnej $ X_ {nowy} $, model OLS przewiduje, jaka zmienna zależna byłaby $ \ hat {Y} _ {new} $ w typowym przypadku.

Chodzi o to, że $ \ hat {Y} _i $ zwykle nie jest uważane za „lepsze” niż $ Y_i $, ale jest raczej dokładniejszym odzwierciedleniem tego, czego oczekujesz, że $ Y $ będzie miało określoną wartość za $ X $ .

Jednak są sytuacje, w których możesz pomyśleć, że $ \ hat {Y} _i $ dokładniej odzwierciedla prawdę niż $ Y_i $ (być może w przypadku wartości odstającej wynikającej z nieprawidłowego działania Twojego zbioru danych). Byłoby to w dużym stopniu zależne od szczegółów Twoich danych.

Czy to pomaga? (To właśnie przyszło mi do głowy po przeczytaniu pytania).

W statystyce twierdzenie Gaussa – Markowa, nazwane na cześć Carla Friedricha Gaussa i Andreya Markova, stwierdza, że ​​w modelu regresji liniowej gdzie błędy mają oczekiwanie zero i są nieskorelowane i mają równe wariancje, najlepszy liniowy nieobciążony estymator (NIEBIESKI) współczynników jest podawany przez zwykły estymator najmniejszych kwadratów (OLS). Tutaj „najlepsze” oznacza podawanie najniższej wariancji oszacowania w porównaniu z innymi nieobciążonymi, liniowymi szacunkami. Błędy nie muszą być normalne, niezależne i identycznie rozmieszczone (tylko nieskorelowane i homoskedastyczne). Hipoteza, że ​​estymator jest bezstronny, nie może zostać odrzucona, ponieważ w przeciwnym razie istnieją estymatory lepsze niż OLS.

http://en.wikipedia.org/wiki/Gauss%E2%80%93Markov_theorem