Jest kilka punktów, które możesz poprawić w kodzie

Niewłaściwe warunki brzegowe

Twój model jest ustalony na I = 1 dla czasu zero. Możesz albo zmienić ten punkt na obserwowaną wartość, albo dodać parametr do modelu, który odpowiednio przesunie czas.

  init <- c (S = N-1, I = 1, R = 0)

# Powinien być

init <- c (S = N-zainfekowany [1], I = zainfekowany [1], R = 0)
 

Nierówne skale parametrów

Jak zauważyli inni ludzie

$$ I '= \ beta \ cdot S \ cdot I - \ gamma \ cdot I $$

ma bardzo dużą wartość dla $ S \ cdot I $ , co powoduje, że wartość parametru $ \ beta $ jest bardzo małe, a algorytm, który sprawdza, czy rozmiary kroków w iteracjach osiągną jakiś punkt, nie zmieni kroków w $ \ beta $ i $ \ gamma $ jednakowo (zmiany w $ \ beta $ będą miały znacznie większy wpływ niż zmiany w $ \ gamma $ ).

Możesz zmienić skalę w wywołaniu funkcji optim , aby skorygować te różnice w rozmiarze (a sprawdzenie hessianu pozwala zobaczyć, czy działa trochę). Odbywa się to za pomocą parametru kontrolnego. Ponadto możesz chcieć rozwiązać funkcję w oddzielnych krokach, dzięki czemu optymalizacja dwóch parametrów jest niezależna od siebie (zobacz więcej tutaj: Jak radzić sobie z niestabilnymi szacunkami podczas dopasowywania krzywej? jest to również wykonywane w kod poniżej, a wynikiem jest znacznie lepsza zbieżność; chociaż nadal osiągasz granice swoich dolnych i górnych granic)

  Opt <- optim (c (2 * współczynniki (mod) [2] / N, współczynniki (mod) [2]), RSS.SIR, method = "L-BFGS-B", lower = dolny, górny = górny,
         hessian = TRUE, control = list (parscale = c (1 / N, 1), factr = 1))
 

bardziej intuicyjne może być skalowanie parametru w funkcji (zwróć uwagę na termin beta / N zamiast beta )

  SIR <- funkcja (czas, stan, parametry) {
  par <- as.list (c (stan, parametry))
  gdzie (par, {dS <- -beta / N * S * I
  dI <- beta / N * S * I - gamma * I
  dR <- gamma * I
  list (c (dS, dI, dR))
  })
}
 

Warunek początkowy

Ponieważ wartość $ S $ jest na początku mniej więcej stała (czyli $ S \ ok. N $ ) wyrażenie dla zarażonych na początku można rozwiązać za pomocą pojedynczego równania:

$$ I '\ approx (\ beta \ cdot N - \ gamma) \ cdot I $$

Więc możesz znaleźć warunek początkowy, używając początkowego dopasowania wykładniczego:

  # uzyskaj dobry stan początkowy
mod <- nls (Zainfekowany ~ a * exp (b * dzień),
           start = list (a = Zainfekowany [1],
                        b = log (zainfekowany [2] / zainfekowany [1])))
 

Niestabilne, korelacja między $ \ beta $ i $ \ gamma $

Jest trochę niejasności, jak wybrać $ \ beta $ i $ \ gamma $ dla warunek początkowy.

To również spowoduje, że wynik analizy nie będzie tak stabilny. Błąd w poszczególnych parametrach $ \ beta $ i $ \ gamma $ będzie bardzo duży, ponieważ wiele par $ \ beta $ i $ \ gamma $ dadzą mniej więcej podobnie niski RSS.

Poniższy wykres dotyczy rozwiązania $ \ beta = 0.8310849; \ gamma = 0,4137507 $

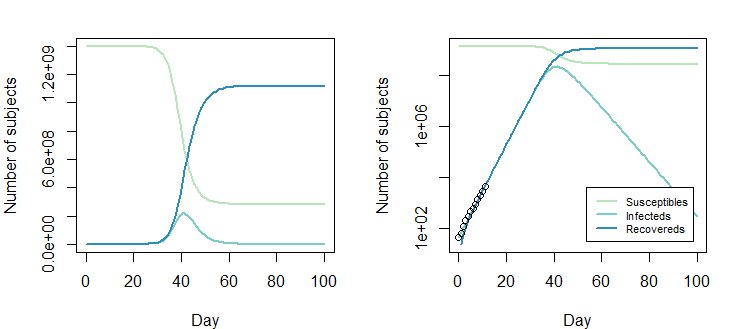
Jednak skorygowana wartość Opt_par $ \ beta = 0.8310849-0.2; \ gamma = 0,4137507-0,2 $ działa równie dobrze:

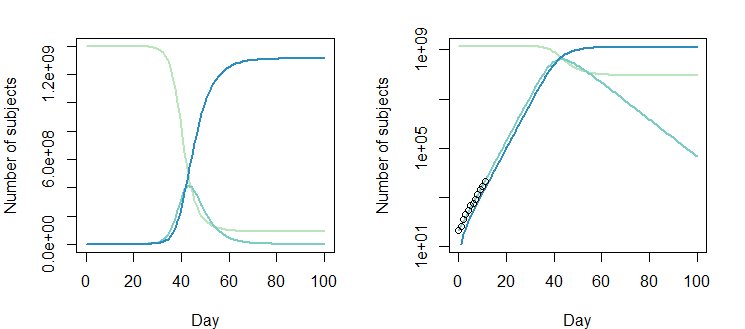
Korzystanie z innej parametryzacji

Funkcja optymalizacji pozwala odczytać hessian

  > Opt <- optim (optimsstart, RSS.SIR, method = "L-BFGS-B", lower = lower, upper = upper,)
+ hessian = TRUE)
> Opt $ hessian
            b
b 7371274104-7371294772
  -7371294772 7371315619
 

Hesja może być powiązana z wariancją parametrów ( W R, mając dane wyjściowe z optyma z macierzą Hesji, jak obliczyć przedziały ufności parametrów przy użyciu macierzy hessiana?). Należy jednak pamiętać, że do tego celu potrzebny jest Hesjan prawdopodobieństwa dziennika, który nie jest taki sam jak RSS (różni się o czynnik, zobacz kod poniżej).

Na tej podstawie można zobaczyć, że oszacowanie wariancji próbki parametrów jest bardzo duże (co oznacza, że ​​wyniki / szacunki nie są zbyt dokładne). Należy jednak pamiętać, że błąd jest silnie skorelowany. Oznacza to, że możesz zmienić parametry tak, aby wynik nie był bardzo skorelowany. Oto kilka przykładów parametryzacji:

$$ \ begin {array} {} c & = & \ beta - \ gamma \\ R_0 & = & \ frac {\ beta} {\ gamma} \ end {array} $$

takie, że stare równania (zwróć uwagę na skalowanie o 1 / N):

$$ \ begin {array} {rccl} S ^ \ prime & = & - \ beta \ frac {S} {N} & I \\ I ^ \ prime & = & (\ beta \ frac {S} {N} - \ gamma) & I \\ R ^ \ prime & = & \ gamma &I \ end {tablica} $$

stać się

$$ \ begin {array} {rccl} S ^ \ prime & = & -c \ frac {R_0} {R_0-1} \ frac {S} {N} & I& \\ I ^ \ prime & = & c \ frac {(S / N) R_0 - 1} {R_0-1} &I& \ underbrace {\ approx c I} _ {\ text {for $ t = 0 $, gdy $ S / N \ około 1 $}} \\ R ^ \ prime & = & c \ frac {1} {R_0-1} & I& \ end {tablica} $$

co jest szczególnie atrakcyjne, ponieważ na początku otrzymujesz ten przybliżony $ I ^ \ prime = cI $ . To to sprawi, że zobaczysz, że zasadniczo szacujesz pierwszą część, która jest w przybliżeniu wykładniczym wzrostem. Będziesz mógł bardzo dokładnie określić parametr wzrostu, $ c = \ beta - \ gamma $ . Jednak $ \ beta $ i $ \ gamma $ lub $ R_0 $ , nie można nie łatwo ustalić.

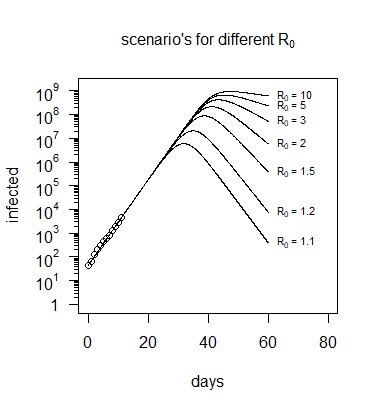
W poniższym kodzie symulacja jest wykonana z tą samą wartością $ c = \ beta - \ gamma $ , ale z różnymi wartościami dla $ R_0 = \ beta / \ gamma $ . Widać, że dane nie są w stanie pozwolić nam rozróżnić, z jakimi różnymi scenariuszami (z jakim różnym $ R_0 $ ) mamy do czynienia (potrzebowalibyśmy więcej informacji, np lokalizacje każdej zainfekowanej osoby i próba sprawdzenia, jak infekcja się rozprzestrzeniła).

Interesujące jest to, że w kilku artykułach udaje się, że mają rozsądne szacunki $ R_0 $ . Na przykład ten wstępny wydruk Nowy koronawirus 2019-nCoV: wczesne oszacowanie parametrów epidemiologicznych i prognoz epidemiologicznych ( https://doi.org/10.1101/2020.01.23.20018549)

Jakiś kod:

  ####
####
####

biblioteka (deSolve)
biblioteka (RColorBrewer)

#https: //en.wikipedia.org/wiki/Timeline_of_the_2019%E2%80%9320_Wuhan_coronavirus_outbreak#Cases_Chronology_in_Mainland_China
Zainfekowany <- c (45, 62, 121, 198, 291, 440, 571, 830, 1287, 1975, 2744, 4515)
dzień <- 0: (długość (zainfekowany) -1)
N <- 1400000000 #pop of China

### edycja 1: użyj innego warunku granicznego
### init <- c (S = N-1, I = 1, R = 0)
init <- c (S = N-zainfekowany [1], I = zainfekowany [1], R = 0)
działka (dzień, zarażony)

SIR <- funkcja (czas, stan, parametry) {
  par <- as.list (c (stan, parametry))
  #### edytuj 2; używaj zmiennych o jednakowej skali
  gdzie (par, {dS <- -beta * (S / N) * I
  dI <- beta * (S / N) * I - gamma * I
  dR <- gamma * I
  list (c (dS, dI, dR))
  })
}

SIR2 <- funkcja (czas, stan, parametry) {
  par <- as.list (c (stan, parametry))
  ####
  #### użyj jako zmiany zmiennej zmiennej
  #### const = (beta-gamma)
  #### delta = gamma / beta
  #### R0 = beta / gamma > 1
  ####
  #### beta-gamma = beta * (1-delta)
  #### beta-gamma = beta * (1-1 / R0)
  #### gamma = beta / R0
  z (par, {
    beta <- const / (1-1 / R0)
    gamma <- const / (R0-1)
    dS <- - (beta * (S / N)) * I
    dI <- (beta * (S / N) -gamma) * I
    dR <- (gamma) * I
    list (c (dS, dI, dR))
  })
}

RSS.SIR2 <- funkcja (parametry) {
  nazwy (parametry) <- c ("const", "R0")
  out <- ode (y = init, times = day, func = SIR2, parms = parameters)
  fit <- out [, 3]
  RSS <- sum ((Zainfekowany - pasuje) ^ 2)
  powrót (RSS)
}

### wykreślanie różnych wartości R0

# użyć zwykłego modelu wykładniczego do określenia const = beta - gamma
const <- coef (mod) [2]




RSS.SIR <- funkcja (parametry) {
  nazwy (parametry) <- c ("beta", "gamma")
  out <- ode (y = init, times = day, func = SIR, parms = parameters)
  fit <- out [, 3]
  RSS <- sum ((Zainfekowany - pasuje) ^ 2)
  powrót (RSS)
}

niższy = c (0, 0)
upper = c (1, 1) ### dostosuj limit, ponieważ inna skala 1 / N

### edycja: uzyskaj dobry stan początkowy
mod <- nls (Zainfekowany ~ a * exp (b * dzień),
           start = list (a = Zainfekowany [1],
                        b = log (zainfekowany [2] / zainfekowany [1])))
optimsstart <- c (2,1) * coef (mod) [2]

set.seed (12)
Opt <- optim (optimsstart, RSS.SIR, metoda = "L-BFGS-B", dolny = dolny, górny = górny,
             hessian = TRUE)
Optować

### oszacowana macierz kowariancji współczynników
### zwróć uwagę na duży błąd, ale także silną korelację (prawie 1)
## zwróć uwagę na skalowanie z oszacowaniem sigma, ponieważ musimy użyć Hessianu loglikeli wiarygodności
sigest <- sqrt (Opt  $ value / (length (Infected) -1))
rozwiązać (1 / (2 * sigest ^ 2) * Opt $  hessian)

####
#### używając alternatywnych parametrów
#### do tego używamy funkcji SIR2
####

optimsstart <- c (coef (mod) [2], 5)
niższy = c (0, 1)
upper = c (1, 10 ^ 3) ### dostosuj limit, ponieważ używamy teraz R0, które powinno być >1

set.seed (12)
Opt2 <- optim (optimsstart, RSS.SIR2, method = "L-BFGS-B"), lower = lower, upper = upper,
              hessian = TRUE, control = list (maxit = 1000,
                                             parscale = c (10 ^ -3,1)))
Opcja 2

# teraz szacowana wariancja pierwszego parametru jest mała
# drugi parametr jest nadal z dużą zmiennością
#
# dzięki temu możemy bardzo dobrze przewidzieć beta - gamma
# ta beta - gamma jest początkowym współczynnikiem wzrostu
# ale indywidualne wartości beta i gamma nie są zbyt dobrze znane
#
# Zauważ również, że hessian nie znajduje się na MLE, ponieważ osiągnęliśmy dolną granicę
#
sigest <- sqrt (Opt2  $ value / (length (Infected) -1))
rozwiąż (1 / (2 * sigest ^ 2) * Opt2 $  hessian)

#### Możemy również oszacować wariancję według
#### Oszacowanie Monte Carlo
##
## zakładając, że dane mają być dystrybuowane jako średnia +/- q średnia
## z q takie, które oznacza RSS = 52030
##
##
##


### Dwie funkcje RSS do optymalizacji w zagnieżdżony sposób
RSS.SIRMC2 <- funkcja (const, R0) {
  parametry <- c (const = const, R0 = R0)
  out <- ode (y = init, times = day, func = SIR2, parms = parameters)
fit <- out [, 3]
  RSS <- sum ((Infected_MC - fit) ^ 2)
  powrót (RSS)
}
RSS.SIRMC <- funkcja (const) {
  optymalizuj (RSS.SIRMC2, lower = 1, upper = 10 ^ 5, const = const) $ goal
}

getOptim <- function () {
  opt1 < - optymalizacja (RSS.SIRMC, dolna = 0, górna = 1)
  opt2 <- optymalizuj (RSS.SIRMC2, lower = 1, upper = 10 ^ 5, const = opt1  $ minimum)
  return (list (RSS = opt2 $  goal, const = opt1  $ minimum, R0 = opt2 $  minimum))
}

# wymodelowanych danych, których używamy do wielokrotnego generowania danych z szumem
Opt_par < - Opt2  $ par
nazwy (Opt_par) <- c ("const", "R0")
modInfected <- data.frame (ode (y = init, times = day, func = SIR2, parms = Opt_par)) $  I

# wykonanie zagnieżdżonego modelu w celu uzyskania RSS
set.seed (1)
Infected_MC < - Infected
modnested <- getOptim ()

errrate <- modnested $ RSS / sum (zainfekowany)


par <- c (0,0)
for (i in 1: 100) {
  Infected_MC <- rnorm (length (modInfected), modInfected, (modInfected * errrate) ^ 0.5)
  OptMC <- getOptim ()
  par <- rbind (par, c (OptMC  $ const, OptMC $  R0))
}
par <- par [-1,]

plot (par, xlab = "const", ylab = "R0", ylim = c (1,1))
tytuł („symulacja Monte Carlo”)
cov (par)


Wniosek ###: parametru R0 nie można wiarygodnie oszacować

##### Koniec estymacji Monte Carlo


### wykreślanie różnych wartości R0

# użyć zwykłego modelu wykładniczego do określenia const = beta - gamma
const <- coef (mod) [2]
R0 <- 1.1

# wykres
plot (-100, -100, xlim = c (0,80), ylim = c (1, N), log = "y",
     ylab = "zainfekowany", xlab = "dni", yaxt = "n")
oś (2, las = 2, at = 10 ^ c (0: 9),
     etykiety = c (wyrażenie (1),
              wyrażenie (10 ^ 1),
              wyrażenie (10 ^ 2),
              wyrażenie (10 ^ 3),
              wyrażenie (10 ^ 4),
              wyrażenie (10 ^ 5),
              wyrażenie (10 ^ 6),
              wyrażenie (10 ^ 7),
              wyrażenie (10 ^ 8),
wyrażenie (10 ^ 9)))
oś (2, at = rep (c (2: 9), 9) * rep (10 ^ c (0: 8), each = 8), labels = rep ("", 8 * 9), tck = -0,02 )
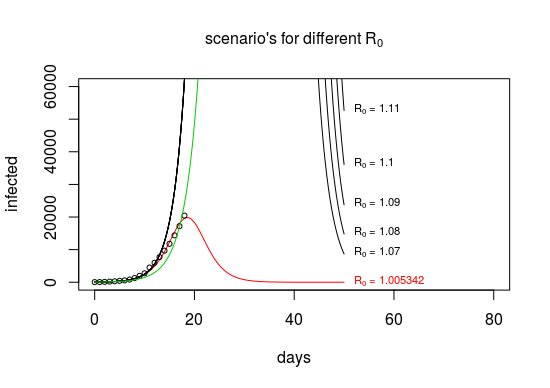
title (bquote (paste ("scenariusze dla różnych", R [0])), cex.main = 1)

# raz
t <- seq (0,60,0,1)

# model działki z różnym R0
dla (R0 in c (1.1,1.2,1.5,2,3,5,10)) {
  fit <- data.frame (ode (y = init, times = t, func = SIR2, parms = c (const, R0))) $ I
  linie (t, fit)
  tekst (t [601], dopasowanie [601],
       bquote (wklej (R [0], "=",. (R0))),
       cex = 0,7, pos = 4)
}

# obserwacji wykresu
punkty (dzień, zainfekowany)
 

Jak szacuje się R0?

Powyższy wykres (powtórzony poniżej) pokazał, że nie ma dużej zmienności liczby „zainfekowanych” w funkcji $ R_0 $ , a dane dotyczące liczby zarażonych osób nie dostarczają zbyt wielu informacji o $ R_0 $ (poza tym, czy jest powyżej lub poniżej zera).

Jednak w przypadku modelu SIR występuje duża zmienność liczby wyzdrowień lub stosunku zakażenia / wyzdrowienia. Jest to pokazane na poniższym obrazku, na którym model jest wykreślany nie tylko pod kątem liczby zarażonych osób, ale także liczby odzyskanych osób. To właśnie takie informacje (a także dodatkowe dane, takie jak szczegółowe informacje, gdzie i kiedy ludzie zostali zainfekowani iz kim mieli kontakt) pozwalają oszacować $ R_0 $ .

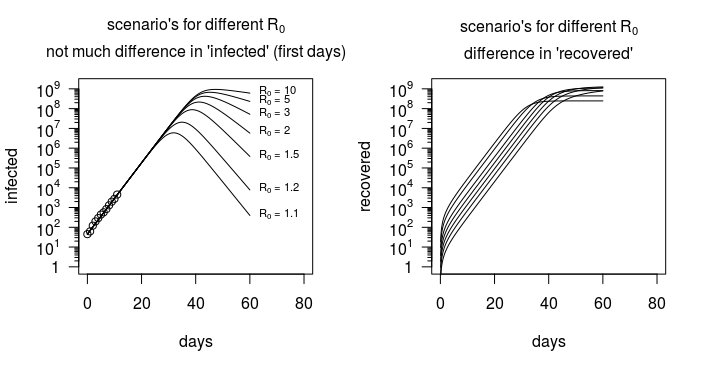
Aktualizacja

W swoim artykule na blogu piszesz, że dopasowanie prowadzi do wartości $ R_0 \ około 2 $ .

Jednak to nie jest właściwe rozwiązanie. Znajdziesz tę wartość tylko dlatego, że optim kończy pracę wcześnie, gdy znajdzie wystarczająco dobre rozwiązanie i ulepszenia dla danego rozmiaru kroku wektora $ \ beta, \ gamma $ stają się małe.

Jeśli korzystasz z optymalizacji zagnieżdżonej, znajdziesz bardziej precyzyjne rozwiązanie z wartością $ R_0 $ bardzo bliską 1.

Widzimy tę wartość $ R_0 \ około 1 $ , ponieważ w ten sposób (nieprawidłowy) model może wprowadzić tę zmianę tempa wzrostu do krzywej.

  ###
####
####

biblioteka (deSolve)
biblioteka (RColorBrewer)

#https: //en.wikipedia.org/wiki/Timeline_of_the_2019%E2%80%9320_Wuhan_coronavirus_outbreak#Cases_Chronology_in_Mainland_China
Zainfekowany <- c (45.62.121.198.291.440.571.830, 1287, 1975,
              2744,4515,5974,7711,9692,11791,14380,17205,20440)
#Infected <- c (45.62.121.198.291.440.571.830, 1287, 1975,
# 2744,4515,5974,7711,9692,11791,14380,17205,20440,
# 24324,28018,31161,34546,37198,40171,42638,44653)
dzień <- 0: (długość (zainfekowany) -1)
N <- 1400000000 #pop of China

init <- c (S = N-zainfekowany [1], I = zainfekowany [1], R = 0)

# funkcja modelu
SIR2 <- funkcja (czas, stan, parametry) {
  par <- as.list (c (stan, parametry))
  z (par, {
    beta <- const / (1-1 / R0)
    gamma <- const / (R0-1)
    dS <- - (beta * (S / N)) * I
    dI <- (beta * (S / N) -gamma) * I
    dR <- (gamma) * I
    list (c (dS, dI, dR))
  })
}

### Dwie funkcje RSS do optymalizacji w zagnieżdżony sposób
RSS.SIRMC2 <- funkcja (R0, const) {
  parametry <- c (const = const, R0 = R0)
  out <- ode (y = init, times = day, func = SIR2, parms = parameters)
  fit <- out [, 3]
  RSS <- sum ((Infected_MC - fit) ^ 2)
  powrót (RSS)
}

RSS.SIRMC <- funkcja (const) {
  optymalizuj (RSS.SIRMC2, lower = 1, upper = 10 ^ 5, const = const) $ goal
}

# opakowanie do optymalizacji i zwracania szacunkowych wartości
getOptim <- function () {
  opt1 < - optymalizacja (RSS.SIRMC, dolna = 0, górna = 1)
opt2 <- optymalizuj (RSS.SIRMC2, lower = 1, upper = 10 ^ 5, const = opt1  $ minimum)
  return (list (RSS = opt2 $  goal, const = opt1  $ minimum, R0 = opt2 $  minimum))
}

# wykonanie zagnieżdżonego modelu w celu uzyskania RSS
Infected_MC < - Infected
modnested <- getOptim ()

rss <- sapply (seq (0.3,0.5,0.01),
       FUN = function (x) optimize (RSS.SIRMC2, lower = 1, upper = 10 ^ 5, const = x) $ goal)

działka (seq (0.3,0.5,0.01), rss)

optymalizuj (RSS.SIRMC2, lower = 1, upper = 10 ^ 5, const = 0,35)


# widok
modnested

### wykreślanie różnych wartości R0

const <- modnested  $ const
R0 <- modnested $  R0

# wykres
plot (-100, -100, xlim = c (0,80), ylim = c (1,6 * 10 ^ 4), log = "",
     ylab = "zainfekowany", xlab = "dni")
title (bquote (paste ("scenariusze dla różnych", R [0])), cex.main = 1)

### to jest twoja wersja beta i gamma z bloga
beta = 0,6746089
gamma = 0,3253912
fit <- data.frame (ode (y = init, times = t, func = SIR, parms = c (beta, gamma))) $ I
linie (t, fit, col = 3)

# model działki z różnym R0
t <- seq (0,50,0,1)
for (R0 in c (modnested  $ R0,1.07,1.08,1.09,1.1,1.11)) {
  fit <- data.frame (ode (y = init, times = t, func = SIR2, parms = c (const, R0))) $ I
  linie (t, fit, col = 1 + (modnested $ R0 == R0))
  tekst (t [501], dopasowanie [501],
       bquote (wklej (R [0], "=",. (R0))),
       cex = 0.7, pos = 4, col = 1 + (modnested $  R0 == R0))
}

# obserwacji wykresu
punkty (dzień, zainfekowany, cex = 0,7)
 

Jeśli użyjemy relacji między wyleczonymi i zainfekowanymi ludźmi $ R ^ \ prime = c (R_0-1) ^ {- 1} I $ , to zobaczymy również odwrotnie, czyli duży $ R_0 $ o wielkości około 18:

  I <- c (45,62,121,198,291,440,571,830,1287,1975,2744,4515,5974,7711,9692,11791,14380,17205,20440, 24324,28018,31161,34546,37198,40171,42638 44653)
D <- c (2,2,2,3,6,9,17,25,41,56,80,106,132,170,213,259,304,361,425,490,563,637,722,811,908,1016,1113)
R <- c (12,15,19,25,25,25,25,34,38,49,51,60,103,124,171,243,328,475,632,892,1153,1540,2050,2649,3281,3996,4749)
A <- I-D-R

wykres (A [-27], różn. (R + D))
mod <- lm (diff (R + D) ~ A [-27])
 

dawanie:

  > const
[1] 0,3577354
> const / mod $ współczynniki [2] +1
  A [-27]
17,87653
 

To jest ograniczenie modelu SIR, który modeluje $ R_0 = \ frac {\ beta} {\ gamma} $ , gdzie $ \ gamma $ wydaje się być mały (bez względu na model, którego używasz).

Mogą występować problemy liczbowe ze względu na bardzo duży rozmiar populacji N $ N $ , co wymusi oszacowanie $ \ beta $ ma być bardzo bliskie zeru.Możesz ponownie sparametryzować model jako \ begin {align} {\ mathrm d S \ over \ mathrm d t} & = - \ beta {S I / N} \\ [1.5ex] {\ mathrm d I \ over \ mathrm d t} & = \ beta {S I / N} - \ gamma I \\ [1.5ex] {\ mathrm d R \ over \ mathrm d t} & = \ gamma I \\ \ end {align}

Dzięki temu oszacowanie $ \ beta $ będzie większe, więc miejmy nadzieję, że dzięki optymalizacji uzyskasz coś sensowniejszego.

W tym kontekście model SIR jest użyteczny, ale daje tylko bardzo przybliżone dopasowanie do tych danych (zakłada, że ​​cała populacja Chin jest jednorodna). Być może nie jest tak źle, jak pierwsza próba analizy. Idealnie byłoby, gdybyś potrzebował jakiegoś modelu przestrzennego lub sieciowego, który lepiej odzwierciedlałby prawdziwą strukturę kontaktów w populacji. Na przykład model metapopulacji opisany w Programie 7.2 i książce towarzyszącej ( Modeling Infectious Diseases in Humans and Animals , Keeling & Rohani). Jednak takie podejście wymagałoby znacznie więcej pracy, a także pewnych danych na temat struktury populacji. Przybliżoną alternatywą może być zastąpienie $ I $ w $ \ beta SI / N $ (w obu dwóch pierwszych równań) z $ I ^ \ delta $ , gdzie $ \ delta $ , czyli prawdopodobnie $ <1 $ to trzeci parametr do oszacowania. Taki model stara się uchwycić fakt, że siła infekcji na podatnym rośnie mniej niż liniowo wraz z liczbą zarażonych $ I $ , unikając przy tym określenia jednoznacznej populacji Struktura. Więcej informacji na temat tego podejścia można znaleźć np. Hochberg, nieliniowe szybkości transmisji i dynamika chorób zakaźnych , Journal of Theoretical Biology 153: 301-321.

Ponieważ populacja Chin jest tak duża, parametry będą bardzo małe.

Ponieważ jesteśmy na początku infekcji, a N jest tak duże, to $ S (t) I (t) / N \ ll 1 $ span>.Mógłbym rozsądniej założyć, że na tym etapie infekcji liczba zarażonych osób jest w przybliżeniu wykładnicza i pasuje do znacznie prostszego modelu.

Jest to tylko w niewielkim stopniu związane ze szczegółową dyskusją na temat kodowania, ale wydaje się bardzo istotne dla pierwotnego pytania dotyczącego modelowania obecnej epidemii 2019-nCoV.Proszę zapoznać się z arxiv: 2002.00418v1 (publikacja na https://arxiv.org/pdf/2002.00418v1.pdf), gdzie przedstawiono model 5-składnikowych równań opóźnionej różnicy, z estymacją parametrów i prognozami przy użyciu dde23 wMatLab.Są one porównywane z publikowanymi codziennie raportami potwierdzonych przypadków, liczby wyleczonych itp. Według mnie jest to całkiem warte omówienia, udoskonalenia i aktualizacji.W konkluzji stwierdza się, że istnieje bifurkacja w przestrzeni rozwiązań zależna od skuteczności izolacji, co wyjaśnia ostatnio podjęte zdecydowane środki w zakresie zdrowia publicznego, które jak dotąd mają duże szanse powodzenia.

co myślisz o umieszczeniu początkowej liczby zakaźnych jako dodatkowego parametru w problemie optymalizacji, w przeciwnym razie dopasowanie musi rozpocząć się od warunku początkowego.