W odpowiedzi na pytanie w komentarzach, oto zarys kilku potencjalnie * szybszych sposobów tworzenia dyskretnych dystrybucji niż metoda cdf.
* Mówię „potencjalnie”, ponieważ w niektórych dyskretnych przypadkach dobrze zaimplementowane podejście odwrotnego CDF może być bardzo szybkie. Ogólny przypadek jest trudniejszy do wykonania szybko bez wprowadzania dodatkowych sztuczek.
W przypadku czterech różnych wyników, jak w przykładzie w pytaniu, naiwna wersja podejścia odwrotnego CDF (lub efektywnie równoważnych podejść) to w porządku; ale jeśli istnieją setki (lub tysiące lub miliony) kategorii, może to stać się powolne, nie będąc trochę mądrzejszym (z pewnością nie chcesz przeszukiwać cdf sekwencyjnie , dopóki nie znajdziesz pierwszej kategorii w którym cdf przekracza losowy uniform). Istnieje kilka szybszych podejść niż to.
[Możesz zobaczyć kilka pierwszych rzeczy, o których wspomniałem poniżej, związanych z szybszymi niż sekwencyjnymi podejściami do lokalizowania wartości za pomocą indeksu i tak jest w pewnym sensie po prostu „mądrzejsza wersja korzystania z cdf”. Można oczywiście spojrzeć na „standardowe” podejścia do rozwiązywania pokrewnych problemów, takie jak „przeszukiwanie posortowanego pliku”, i skończyć z metodami o wiele szybszymi niż sekwencyjne; jeśli możesz wywołać odpowiednie funkcje, takie standardowe podejścia mogą często być wszystkim, czego potrzebujesz.]
W każdym razie do wydajnych metod generowania z dystrybucji dyskretnych.
1 ) „Metoda tabelowa”. Zamiast $ O (n) $ dla kategorii $ n $ , po skonfigurowaniu Wersja tego w (a) (jeśli dystrybucja jest odpowiednia) to $ O (1) $ .
a) Proste podejście - zakładanie racjonalnych prawdopodobieństw (wykonane na powyższym przykładzie danych):
- skonfiguruj tablicę z 10 komórkami, zawierającą „1”, cztery „2”, dwie „3” i trzy „4”. Wypróbuj to, używając dyskretnego munduru (łatwe do zrobienia z ciągłego munduru), a otrzymasz prosty, szybki kod.
b) Przypadek bardziej złożony - nie potrzebuje „ładnych” prawdopodobieństw. Użyj komórek 2 ^ k $ , a raczej zużyjesz kilka mniej. Rozważmy na przykład następujące kwestie:
x 0 1 2 3 4 5 6P (X = x) 0,4581 0,0032 0,1985 0,3298 0,0022 0,0080 0,0002
( Moglibyśmy oczywiście mieć 10000 komórek i użyć poprzedniego dokładnego podejścia, ale co, jeśli te prawdopodobieństwa są, powiedzmy, irracjonalne? . Pomnóż prawdopodobieństwa przez $ 2 ^ k $ i obetnij, aby dowiedzieć się, ile komórek każdego typu potrzebujemy:
x 0 1 2 3 4 5 6 TotP (X = x) 0,4581 0,0032 0,1985 0,3298 0,0022 0,0080 0,0002 1,0000 [256p (x)] 117 0 50 84 0 2 0 253
Następnie ostatnie 3 komórki są w zasadzie „generuj zamiast tego z tej innej dystrybucji” (tj. p (x) - \ frac {\ lfloor 256 p (x) \ rfloor} {256} znormalizowane do pliku pmf):
x * 0 1 2 3 4 5 6 TotP (X = x *) 0,091200 0,273067 0,272000 0,142933 0,187733 0,016000 0,017067 1,000000
Tabelę „spillover” można wykonać dowolną rozsądną metodą (dostajesz się tutaj tylko w około 1% przypadków, nie musi to być tak szybkie). Tak więc $ \ frac {253} {256} $ czasu, w którym generujemy losowy uniform, używamy jego pierwszych 8 bitów do wybrania losowej komórki i wyprowadzamy wartość w komórka; po wstępnej konfiguracji wszystko to można zrobić bardzo szybko. W innym czasie $ \ frac {3} {256} $ trafiliśmy na komórkę z napisem „generuj z drugiej tabeli”. Prawie zawsze generujesz pojedynczy uniform na $ (0,1) $ i otrzymujesz dyskretną liczbę losową z mnożenia, obcięcia i kosztu dostępu do elementu tablicy.
2) Metoda „podniesienia histogramu do kwadratu”; jest to trochę powiązane z (1), ale każda komórka może w rzeczywistości wygenerować jedną z dwóch wartości, w zależności od (ciągłego) uniformu. Generujesz więc dyskretną wartość od 1 do n, a następnie w każdym z nich sprawdź, czy wygenerować jej główną wartość, czy drugą. Działa z ograniczonymi zmiennymi losowymi. Nie ma tabeli spillover i generalnie używa ona znacznie mniejszych tabel niż metoda (1). Zwykle jest skonfigurowany tak, że wybór 1: n wykorzystuje kilka pierwszych bitów jednolitej liczby losowej, a pozostała część określa, którą z dwóch wartości ma wyprowadzić ten bin.
Być może najprostszym sposobem opisania metody jest zrobienie tego na powyższym przykładzie:
Pomyśl o rozkładzie jako histogramie z 4 przedziałami:
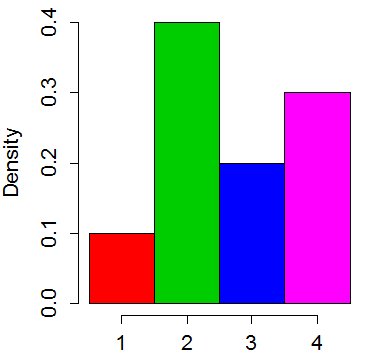
Odcięliśmy szczyty najwyższych prętów i umieściliśmy je w krótszych, „prostując”. Średnia „wysokość” słupka będzie wynosić 0,25. Więc odciąliśmy 0,15 od drugiego taktu i umieściliśmy go w pierwszym i 0,05 poza czwartym i umieściliśmy go w trzecim:
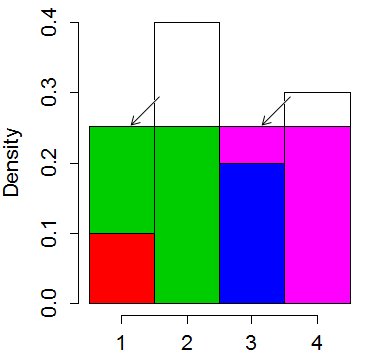
Zawsze można to zorganizować w w taki sposób, że żaden kosz nie kończy się na więcej niż 2 kolorach, chociaż jeden kolor może trafić do kilku pojemników.
Więc teraz wybierasz losowo jeden z 4 pojemników (wymaga 2 losowych bitów z wierzchu munduru). Następnie używasz pozostałych bitów, aby określić równomiernie rozłożone położenie w pionie i porównać z przerwą między kolorami, aby ustalić, którą z dwóch wartości wyprowadzić. Chociaż jest bardzo szybka, zwykle nie jest tak szybka jak metoda „tabelowa”.
-
Te metody można dostosować do obsługi zmiennych nieograniczonych, gdzie znowu jest „przeważnie szybka '.
Odniesienie: http://www.jstatsoft.org/v11/i03/paper
Stosunkowo powolna część z nich to tworzenie tabele wartości; są odpowiednie, gdy wiesz, co będziesz generować („musimy próbkować wartości z tej dystrybucji wiele razy w przyszłości”), zamiast próbować tworzyć to na bieżąco. „Musimy jak najszybciej pobrać próbkę miliona wartości z tego, ale nigdy nie będziemy musieli tego robić ponownie” stwarza inne priorytety; w wielu sytuacjach niektóre ze "standardowych podejść obliczeniowych" do wyszukiwania posortowanych wartości (np. szybsze wykonanie metody cdf) mogą być najlepszym wyborem.
Są jeszcze inne szybkie podejścia do generowania z dyskretnych dystrybucji. Starannie zakodowane, możesz zrobić bardzo szybkie generowanie. Na przykład:
3) metoda odrzucenia („akceptacja-odrzucenie”) może być wykonana z dyskretnymi dystrybucjami; jeśli masz dyskretną funkcję majoralizującą („obwiednię”), która jest skalowanym dyskretnym pmf, z którego możesz już wygenerować w szybki sposób, dostosowuje się ona bezpośrednio, aw niektórych przypadkach może być bardzo szybka. Bardziej ogólnie można skorzystać z możliwości generowania na podstawie ciągłych rozkładów (na przykład dyskretyzując wynik z powrotem do dyskretnej obwiedni).
Tutaj wyobraźmy sobie, że mamy jakąś dyskretną funkcję prawdopodobieństwa $ f $ , dla której nie mamy wygodnego cdf (lub inverse-cdf) - - rzeczywiście na tej ilustracji nie mieliśmy nawet stałej normalizującej, więc nasz wykres jest unormalizowany:

Teraz musimy znaleźć wygodną do wygenerowania funkcję prawdopodobieństwa dyskretnego $ g $ , którą można pomnożyć przez stałą $ c $ i być wszędzie co najmniej tak duże jak $ f $ (musimy być pewni, że to obowiązuje dla wszystkich $ x $ wartości). To znaczy $ cg (x) \ geq f (x) $ dla wszystkich możliwych $ x $ wartości.
Czasami można łatwo zidentyfikować odpowiedni $ g $ , ale jedną z przydatnych opcji jest wybranie mieszanki oddzielnego munduru dla lewej części oraz dystrybucja z co najmniej tak ciężkim ogonem jak $ f $ po prawej stronie. Dwa całkiem dogodne opcje to rozkład geometryczny (kiedy ogon nie zmniejsza się wolniej niż wykładniczo) i coś w rodzaju dyskretyzowanego rozkładu Pareto lub dyskretyzowanego pół-Cauchy'ego, otrzymanego przez wzięcie $ \ lfloor X \ rfloor $ dla jakiejś losowej zmiennej Pareto lub pół-Cauchy'ego $ X $ (w obu przypadkach, gdy pmf spada wolniej niż wykładniczo).
(Sam geometrię można wygenerować poprzez dyskretyzację wykładniczą).
W tym przypadku dyskretny jednolity po lewej i geometryczny po prawej działają całkiem dobrze :
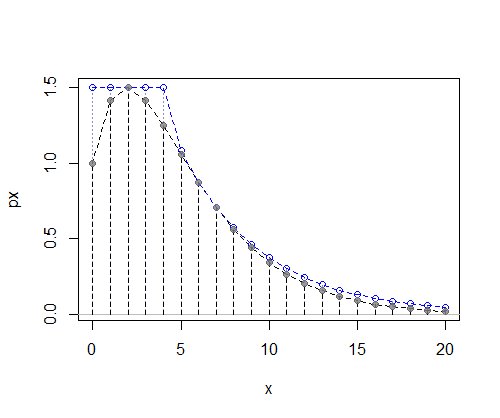
(Przypomnienie: to, co tu wykreślono, to nieznormalizowane pmf, więc oś Y nie przedstawia prawdopodobieństwa, ale coś proporcjonalnego prawdopodobieństwa)
Następnie procedura polega na zasymulowaniu proponowanej wartości $ x $ z $ g $ , symulowanie munduru, $ U $ na $ (0, cg (x)) $ i jeśli $ U<f $ , akceptując proponowany $ x $ (w przeciwnym razie odrzucając go i generując nowy proponowany $ x $ ).