Przykład z normalnymi danymi. Załóżmy, że rzeczywiste dane to losowa próbka o rozmiarze $ n = 200 $ z $ \ mathsf {Norm} (\ mu = 100, \ sigma = 15), $ ale nie znasz $ \ mu $ lub $ \ sigma $ i postaraj się je oszacować. W poniższym przykładzie oszacowałbym wartość $ \ mu $ na podstawie $ \ bar X = 100,21 $ i $ \ sigma $ do $ S = 14,5, $ Oba szacunki są całkiem dobre. (Symulacja i obliczenia w R.)

  set.seed (402) # dla odtwarzalności
x = rnorm (200, 100, 15)
średnia (x); sd (x)
# [1] 100,2051 # aprx 100
# [1] 14.5031 # aprx 15
 

Załóżmy teraz, że brakuje 25% tych danych. (To duża część, ale jestem próbując wskazać punkt.) Jeśli zastąpię brakujące obserwacje średnią ze 150 niebrakujących obserwacji, zobaczmy, jakie są moje oszacowania $ \ mu $ i $ \ sigma $ będzie.

  x.nonmis = x [51: 200] # dla uproszczenia załóżmy, że brakuje pierwszych 50
x.imputd = c (rep (średnia (x.nonmis), 50), x.nonmis)
długość (x.imputd); mean (x.imputd); sd (x.imputd)
# [1] 200 # „x.imputd” ma odpowiednią długość 200
# [1] 100,3445 # aprx 100
# [1] 12,58591 # znacznie mniejszy niż 15
 

Teraz szacujemy $ \ mu $ na $ \ bar X_ {imp} = 100,3, $ co nie jest złym oszacowaniem, ale potencjalnie (jak tutaj) gorzej niż średnia z rzeczywistych danych. Jednak obecnie szacujemy, że $ \ sigma $ jako $ S_ {imp} = 12,6, $ jest dość nieco poniżej zarówno prawdziwego $ \ sigma $ , jak i jego lepszego oszacowania 14,5 z rzeczywistych danych.

Przykład z danymi wykładniczymi. Jeśli dane są mocno przekrzywione w prawo (jak w przypadku danych z populacji wykładniczej), zastąpienie brakujących danych średnią danych bez brakujących danych może maskować skośność, tak aby możemy być zaskoczeni, że dane nie odzwierciedlają tego, jak ciężki jest prawy ogon populacji.

  set.seed (2020) # dla odtwarzalności
x = rexp (200, .01)
średnia (x); sd (x)
# [1] 108.0259 # aprx 100
# [1] 110,1757 # aprx 100
x.nonmis = x [51: 200] # dla uproszczenia załóżmy, że brakuje pierwszych 50
x.imputd = c (rep (średnia (x.nonmis), 50), x.nonmis)
długość (x.imputd); mean (x.imputd); sd (x.imputd)
# [1] 200
# [1] 106,7967 # aprx 100
# [1] 89,21266 # mniejsze niż 100
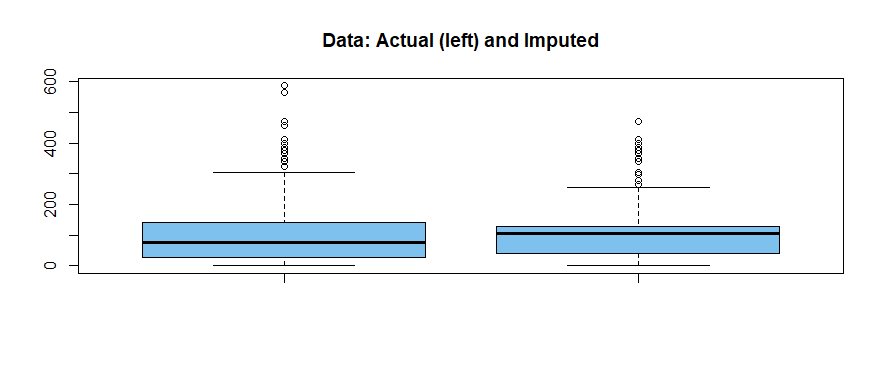
boxplot (x, x.imputd, col = "skyblue2", main = "Dane: rzeczywiste (po lewej) i przypisane")
 

Wykres pudełkowy pokazuje więcej skośności w rzeczywistych danych (wiele obserwacji z dużym ogonem) niż w danych „imputed”.

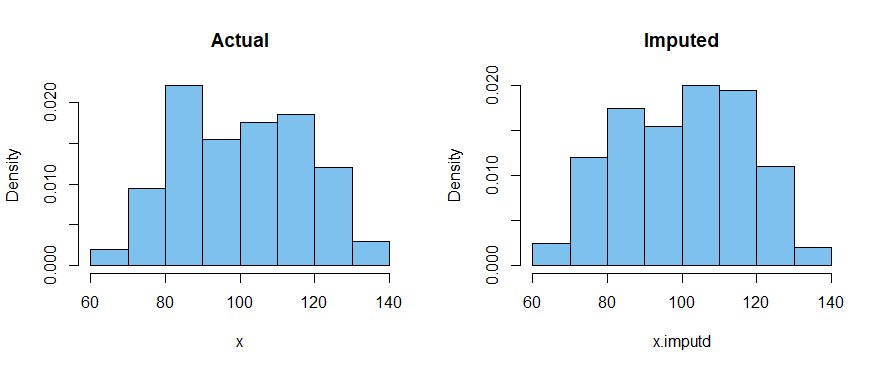
Przykład z danymi bimodalnymi. Ponownie tutaj, kiedy podstawimy brakujące wartości przez średnia z obserwacji bez brakujących danych, odchylenie standardowe populacji jest niedoszacowane. Być może poważniej, duża liczba imputowanych wartości w środku „imputowanej” próbki maskuje bimodalny charakter danych.

  set.seed (1234) # dla odtwarzalności
x1 = rnorm (100, 85, 10); x2 = rnorm (100, 115, 10)
x = próbka (c (x1, x2)) # losowa kolejność mieszania
średnia (x); sd (x)
# [1] 99.42241
# [1] 18.97779
x.nonmis = x [51: 200] # dla uproszczenia załóżmy, że brakuje pierwszych 50
x.imputd = c (rep (średnia (x.nonmis), 50), x.nonmis)
długość (x.imputd); mean (x.imputd); sd (x.imputd)
# [1] 200
# [1] 99.16315
# [1] 16.41451
par (mfrow = c (1,2))
 hist (x, prob = T, col = "skyblue2", main = "Actual")
 hist (x.imputd, prob = T, col = "skyblue2", main = "Imputed")
par (mfrow = c (1,1))
 

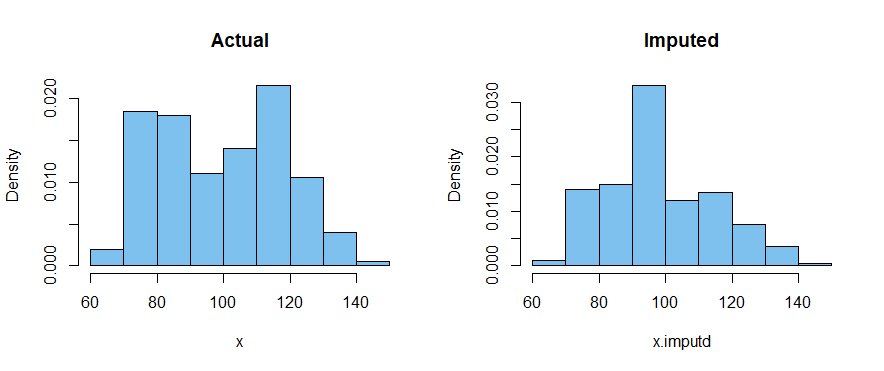
Ogólnie: Zastępowanie brakujących danych średnimi danymi bez brakujących danych powoduje, że SD populacji jest niedoszacowany, ale może również zaciemniać ważne cechy populacji, z której próbkowano dane.

Uwaga: jak zauważa @ benso8, użycie średniej z danych bez brakujących danych w celu zastąpienia brakujących obserwacji jest nie zawsze złym pomysłem. Jak wspomniano w pytaniu, ta metoda ogranicza zmienność. Z pewnością każdy schemat będzie miał wady za radzenie sobie z brakującymi danymi. Pytanie dotyczyło spekulacji na temat możliwych niedogodności innych niż redukcja wariancji dla tej metody. Próbowałem zilustrować kilka możliwości w moich dwóch ostatnich przykładach.

Wstępna metoda alternatywna: nie jestem ekspertem w eksploracji danych. Dlatego bardzo wstępnie proponuję alternatywną metodę. Nie twierdzę, że to nowy pomysł.

Zamiast zastępować wszystkie $ m $ brakujące elementy średnią próbną elementów, których nie brakuje, można wziąć losową próbkę o rozmiarze $ m $ spośród niebrakujących obserwacji i przeskaluj go tak, aby $ m $ elementy miały tę samą średnią i odchylenie standardowe, co niebrakujące dane . Następnie połącz przeskalowane elementy $ m $ z elementami bez brakujących danych, aby otrzymać „przypisaną” próbkę z prawie taką samą średnią i odchyleniem standardowym, co niebrakująca część próbki.

Wynik nie powinien systematycznie lekceważyć SD populacji i może lepiej zachować cechy populacji, takie jak skośność i bimodalność. (Komentarze mile widziane.)

Pomysł ten jest rozważany poniżej dla danych bimodalnych:

  set.seed (4321) # dla odtwarzalności
x1 = rnorm (100, 85, 10); x2 = rnorm (100, 115, 10)
x = próbka (c (x1, x2)) # scrmble
średnia (x); sd (x)
# [1] 100,5299
# [1] 17.03368
x.nonmis = x [51: 200] # dla uproszczenia załóżmy, że brakuje pierwszych 50
an = średnia (x.nonmis); sn = sd (x.nonmis)
x.subt = sample (x.nonmis, 50) # tymczasowe nieskalowane substytuty
as = średnia (xsubt); ss = sd (x.subt)
x.sub = ((x.subt - as) / ss) * sn + an # skalowane podstawniki

x.imputd = c (x.sub, x.nonmis)
mean (x.imputd); sd (x.imputd)
# [1] 100.0694 # aprx to samo co średnia z braku braków
# [1] 16.83213 # aprx to samo SD systemu operacyjnego, co nie brakuje

par (mfrow = c (1,2))
 hist (x, prob = T, col = "skyblue2", main = "Actual")
 hist (x.imputd, prob = T, col = "skyblue2", main = "Imputed")
par (mfrow = c (1,1))
 

Używanie średniej dla brakujących wartości nie jest ZAWSZE złe. W ekonometrii jest to zalecany sposób postępowania w niektórych przypadkach, pod warunkiem, że rozumiesz, jakie mogą być konsekwencje iw jakich przypadkach jest to pomocne. Jak już przeczytałeś, zastąpienie brakujących wartości średnią może zmniejszyć wariancję. Oto, co to może spowodować.

Zwróć uwagę, że w przypadku modeli regresji współczynnik determinacji $$ R ^ 2 = \ frac {SSR} {SSTO} = \ frac {\ sum (\ hat {y_i} - \ bar {y}) ^ 2} {\ sum (y_i - \ bar {y}) ^ 2}. $$ Zakładając, że brakuje $ y $ span > i zastąpisz je średnią próbną, możesz mieć wartość $ R ^ 2 $ , która nie jest tak dokładna, jak w przypadku rzeczywistych danych. Większa wariancja danych oznacza, że ​​jest więcej danych, które prawdopodobnie znajdują się dalej od linii regresji. Ponieważ wartość $ R ^ 2 $ zależy od poszczególnych obserwowanych wartości $ y $ (patrz $ y_i $ w $ SSTO $ ), Twój $ R ^ 2 $ może zostać zawyżone, ponieważ $ SSTO $ będzie mniejszy.

Spójrzmy na przykład.

Załóżmy, że masz wartość $ x_3 $ i odpowiadającą jej obserwacją dla tej $ x $ wartość była $ y_3 $ . Wykonujemy obliczenia dla tego wyniku dla SSTO i mamy

$$ (y_3 - \ bar {y}) ^ 2 $$

i ten wynik zostanie dodany do sumy $ SSTO $ . Zamiast tego powiedzmy, że brakuje wartości $ y_3 $ . Następnie zostawmy brakujący $ y_3 = \ bar {y} $ . Mamy wtedy

$$ (\ bar {y} - \ bar {y}) ^ 2 = 0. $$ .

Jak widać, kiedy dodamy to do innych wyników dla mianownika, suma $ SSTO $ będzie mniejsza.

Inną możliwą wadą stosowania średniej dla brakujących wartości jest to, że przyczyna, dla której brakuje wartości, może przede wszystkim zależeć od samych brakujących wartości.(Nazywa się to brakującym nie przypadkiem).

Na przykład w kwestionariuszu zdrowotnym, ciężsi respondenci mogą być mniej skłonni do ujawnienia swojej wagi.Średnia obserwowanych wartości byłaby niższa niż prawdziwa średnia dla wszystkich respondentów i używałbyś tej wartości zamiast wartości, które w rzeczywistości powinny być znacznie wyższe.

Użycie średniej jest mniejszym problemem, jeśli przyczyna braku wartości jest niezależna od samych brakujących wartości.

Problem nie polega konkretnie na tym, że redukuje wariancję, ale że zmienia wariancję zbioru danych, czyniąc go mniej dokładnym oszacowaniem dla wariancji rzeczywistej populacji. Mówiąc bardziej ogólnie, zbiór danych będzie pod wieloma względami mniej dokładnym odzwierciedleniem populacji.

Warto rozważyć alternatywy. Dlaczego użycie 0 (lub dowolnej innej losowej wartości) dla brakujących punktów byłoby złym pomysłem? Ponieważ zmieniłoby to zestaw danych w sztuczny sposób, sprawiając, że mniej odzwierciedlałby idealną populację, a wnioski wyciągane ze zbioru danych byłyby mniej dokładne. Dlaczego używanie średniej dla brakujących punktów jest mniej złe niż używanie innych wartości? Ponieważ nie zmienia średniej ze zbioru danych - a średnia jest zwykle najważniejszą pojedynczą statystyką. Ale to wciąż tylko jedna statystyka! Cały sens eksploracji danych polega na tym, że zbiór danych a zawiera znacznie więcej informacji poza średnią. Wypełnienie brakujących punktów średnią może wpłynąć na wszystkie pozostałe informacje. Tak więc wypełniony zestaw danych będzie mniej dokładny do wyciągania wniosków dotyczących rzeczywistej populacji. Rozbieżność to tylko jedna konkretna część tych dalszych informacji, która jasno ilustruje zmiany.

„Dlaczego ta redukcja wariancji jest uważana za coś złego?”

Jako nadmiernie uproszczony przykład: wyobraź sobie przez chwilę, że masz niezwykle małą gospodarkę na jakiejś wyspie, z zaledwie 5 osobami.Ich roczne dochody są następujące:

• Osoba 1: ♦ 10 000
• Osoba 2: ♦ 10 000
• Osoba 3: ♦ 12 000
• Osoba 4: ♦ 13 000
• Osoba 5: ♦ 25 000

Firma samochodowa chcąca „włamać się na rynek” decyduje się na wycenę swoich pojazdów na podstawie średnich rocznych zarobków.

Średnia: ♦ 14 000
Mediana: ♦ 12 000
Tryb: ♦ 10 000

Jak widać, użycie trybu może wykluczyć 80% populacji z zakupu ich produktu, co sprawia, że jest to bardzo zły wybór przy tworzeniu uzasadnienia biznesowego!

Tak, lubię pomysł pobierania próbek z rozkładu, w którym występuje wiele braków danych, w celu uzyskania wartości zastępczej dla brakującej wartości k.

Mój wybór to jednak dystrybucja wyśrodkowana na medianie próbki (nie średniej) i z wariancją podaną tutaj https://www.jstor.org/stable/30037287?seq=1.

Być może próbka z obciętej normy na podstawie powyższych parametrów.