Prawdopodobieństwo, że kostka się nie pojawi $ n $ wynosi 1-1 / n $ .Prawdopodobieństwo, że $ n $ nie pojawi się na żadnej z kości $ n $ wynosi $ (1-1 / n) ^ n $ .Jeśli odejmiesz to od 1 $ , prawdopodobnie pojawi się co najmniej jeden $ n $ kiedy rzucasz kostką $ n $ , tj.

$$ p = 1- (1-1 / n) ^ n \ rightarrow 1-e ^ {- 1} $$ jako $ n $ idzie do $ \ infty. $

Wydarzenie $ A: = $ "co najmniej jedna kość pojawia się na boku $ n $ "jest uzupełnieniem zdarzenia $ B: = $ " wszystkie kostki pojawiają się na innym niż $ n $ stron ”.

A więc $ P (A) = 1-P (B) $ . Co to jest $ P (B) $ ?

Wszystkie kości są niezależne, więc

$$ P (\ text {wszystkie $ n $ kości pojawiają się na innych niż $ n $ stronach}) = P (\ text {jedna kostka okazuje się inna niż $ n $}) ^ n = \ bigg (\ frac {n-1} {n} \ bigg) ^ n. $$

Więc

$$ P (A) = 1- \ bigg (\ frac {n-1} {n} \ bigg) ^ n. $$

Ufaj, ale weryfikuj. Lubię to robić w R:

  > nn <- 6
> n_sims <- 1e5
Suma > (replicate (n_sims, any (sample (1: nn, nn, replace = TRUE) == nn))) / n_sims
[1] 0,66355
> 1 - ((nn-1) / nn) ^ nn
[1] 0,665102
 

Wygląda dobrze. Spróbuj tego z innymi wartościami nn . Oto fabuła:

  nn <- 2: 100
plot (nn, 1 - ((nn-1) / nn) ^ nn, type = "o", pch = 19, ylim = c (1-1 / exp (1), 1))
abline (h = 1-1 / exp (1), col = "red")
 

Zwracamy uwagę, jakie jest nasze prawdopodobieństwo w limicie

$$ P (A) = 1- \ bigg (\ frac {n- 1} {n} \ bigg) ^ n = 1- \ bigg (1- \ frac {1} {n} \ bigg) ^ n \ to 1- \ frac {1} {e} \ około 0.6321206 \ quad \ text {as} n \ do \ infty, $$

z powodu tożsamości obejmującej $ e $ .

Odpowiedzi udzielone przez @StephanKolassa (+1) i @gunes (+1) są w porządku. Ale ten problem można rozwiązać w odniesieniu do dwumianu i Poissona dystrybucje w następujący sposób:

Jeśli $ X_n $ to liczba n widocznych w $ n $ span> rolki uczciwej $ n $ jednostronnej kostki, następnie $ X_n \ sim \ mathsf {Binom} (n, 1 / n), $ , aby $ P (X_n \ge 1) = 1 - P (X_n = 0) = 1- (1-1 / n) ^ n. $

Jako $ n \ rightarrow \ infty, $ jeden ma $ X_n \ stackrel {prob} {\ rightarrow} Y\ sim \ mathsf {Pois} (\ lambda = 1), $ z $ P (Y \ ge 1) = 1 - P (Y = 0) = 1 -e ^ {- 1}. $

Odpowiedź można uzyskać, licząc również opisane zdarzenia, chociaż przyjęta odpowiedź jest bardziej elegancka . Rozważymy przypadek kości i miejmy nadzieję, że uogólnienie jest oczywiste. Pozwolimy, aby przestrzeń zdarzenia obejmowała wszystkie sekwencje liczb z $ \ {1,2, ..., 6 \} $ długości 6 $ . Oto kilka przykładów (wybranych losowo):

  3 2 3 5 6 1
1 1 2 5 2 4
1 2 1 1 6 3
4 4 3 3 4 2
6 1 1 6 3 4
6 3 5 4 5 1
 

Chodzi o to, że nasza przestrzeń ma w sumie 6 $ 6 $ zdarzeń, a ze względu na niezależność przypuszczamy, że każde z nich jest równie prawdopodobne jak inne (równomiernie rozłożone). Musimy policzyć, ile sekwencji zawiera co najmniej jedno 6 $ . Dzielimy przestrzeń, którą liczymy, według tego, ile 6 $ pojawi się, więc rozważ przypadek, w którym dokładnie jeden 6 $ pojawia się. Na ile możliwych sposobów może się to stać? Sześć może pojawić się w dowolnej pozycji (6 różnych pozycji), a gdy tak się stanie, pozostałe 5 pozycji może mieć dowolny z 5 różnych symboli (z $ \ {1,2, ... , 5 \} $ ). Wtedy całkowita liczba sekwencji z dokładnie jednym 6 $ wynosi: $ \ binom {6} {1} 5 ^ 5 $ . Podobnie w przypadku, gdy są dokładnie dwa 6 $ : otrzymujemy, że są dokładnie $ \ binom {6} {2} 5 ^ 4 $ takich sekwencji. Teraz czas na zabawę z sumami :

$$ \ sum_ {k = 1} ^ 6 \ binom {6} {k} 5 ^ {6-k} = \ sum_ {k = 0} ^ 6 \ binom {6} {k} 5 ^ {6-k} 1 ^ k - 5 ^ 6 = (5 + 1) ^ 6 - 5 ^ 6 $$

Aby obliczyć prawdopodobieństwo z tej liczby, podzielimy przez całkowitą liczbę zdarzeń:

$$ \ frac {6 ^ 6 - 5 ^ 6} {6 ^ 6} = 1 - (5/6) ^ 6 = 1 - (1-1 / 6 ) ^ 6 $$

Myślę, że to całkiem nieźle uogólnia, ponieważ dla każdego $ n $ innego niż 6 $ ,zachowują dokładnie te same argumenty, tylko zamień każde wystąpienie 6 $ na $ n $ i 5 $ z $ n-1 $ .

Warto również zauważyć, że ta liczba $ 5 ^ 6 = \ binom {6} {0} 5 ^ 6 $ to udział sekwencji, w których nie ma 6 $ występuje i jest znacznie łatwiejsze do obliczenia (zgodnie z przyjętą odpowiedzią).

Uważam, że odpowiedź BruceET jest interesująca, w odniesieniu do liczby zdarzeń. Alternatywnym sposobem rozwiązania tego problemu jest wykorzystanie zależności między czasem oczekiwania a liczbą zdarzeń. Wykorzystanie tego polegałoby na tym, że problem będzie można w pewien sposób łatwiej uogólniać.

Postrzeganie problemu jako problemu związanego z czasem oczekiwania

Ta korespondencja, jak na przykład wyjaśniono / wykorzystano tutaj i tutaj, to

Aby uzyskać liczbę rzutów kośćmi $ m $ i liczbę trafień / zdarzeń $ k $ ty dostać: $$ \ begin {array} {ccc} \ overbrace {P (K \ geq k | m)} ^ {\ text {właśnie tego szukasz}} & = & \ overbrace {P (M \ leq m | k)} ^ {\ text {zamiast tego wyrażamy to}} \\ {\ small \ text {$ \ mathbb {P} $ $ k $ lub więcej wydarzeń w $ m $ dice rolls}} & = & {\ small \ text {$ \ mathbb {P} $ rzuca kostkami poniżej $ m $ podane $ k $ wydarzeń}} \ end {tablica} $$

Słowami: prawdopodobieństwo uzyskania większej liczby zdarzeń niż $ K \ geq k $ (np. $ \ geq 1 $ razy rzucić 6) w ciągu kilku rzutów kośćmi $ m $ równa się prawdopodobieństwu, że będziesz potrzebować $ m $ lub mniej rzutów kośćmi, aby uzyskać $ k $ takich zdarzeń.

To podejście dotyczy wielu dystrybucji

  Dystrybucja dystrybucji
Czas oczekiwania między zdarzeniami liczba zdarzeń

Wykładniczy Poissona
Erlang / Gamma ponad / słabo rozproszony Poissona
Dwumian geometryczny
Ujemny dwumian ponad / zbyt rozproszony dwumianowy
 

Zatem w naszej sytuacji czas oczekiwania jest rozkładem geometrycznym. Prawdopodobieństwo, że liczba rzutów kośćmi $ M $ przed wykonaniem pierwszego $ n $ jest mniejsze niż lub równe $ m $ (i biorąc pod uwagę prawdopodobieństwo wyrzucenia $ n $ równa się 1 $ / n $ ) to następujący CDF dla rozkładu geometrycznego:

$$ P (M \ leq m) = 1- \ left (1- \ frac {1} {n} \ right) ^ m $$

i szukamy sytuacji $ m = n $ , więc otrzymujesz:

$$ P (\ text {w ciągu $ n $ rolek pojawi się $ n $}) = P (M \ leq n) = 1- \ left (1 - \ frac {1} {n} \ right) ^ n $$

Uogólnienia, kiedy $ n \ to \ infty $

Pierwsze uogólnienie jest takie, że dla $ n \ to \ infty $ rozkład liczby zdarzeń staje się Poissona ze współczynnikiem $ \ lambda $ , a czas oczekiwania stanie się rozkładem wykładniczym ze współczynnikiem $ \ lambda $ . Tak więc czas oczekiwania na rzut zdarzeniem w procesie rzutu kośćmi Poissona wynosi $ (1-e ^ {- \ lambda \ times t}) $ i $ t = 1 $ otrzymamy ten sam wynik $ \ około 0,632 $ , co inne odpowiedzi. To uogólnienie nie jest jeszcze tak wyjątkowe, ponieważ odtwarza tylko inne wyniki, ale w przypadku następnego nie widzę bezpośrednio, jak mogłoby działać uogólnienie bez zastanawiania się nad czasem oczekiwania.

Uogólnienia, kiedy kości są niesprawiedliwe

Możesz rozważyć sytuację, w której kostki są niesprawiedliwe. Na przykład raz rzucisz kostką, która ma 0,17 prawdopodobieństwa, że ​​wyrzuci 6, a innym razem kostką, która ma 0,16 prawdopodobieństwa wyrzucenia 6. Oznacza to, że 6 będzie bardziej skupione wokół kości z dodatnim odchyleniem i że prawdopodobieństwo wyrzucenia 6 na 6 zwojów będzie mniejsze niż wartość $ 1-1 / e $ . (oznacza to, że na podstawie średniego prawdopodobieństwa pojedynczego rzutu, powiedzmy, że określiłeś je z próbki wielu rzutów, nie możesz określić prawdopodobieństwa w wielu rzutach tymi samymi kostkami, ponieważ musisz wziąć pod uwagę korelację kości)

Powiedzmy, że kostka nie ma stałego prawdopodobieństwa $ p = 1 / n $ , ale zamiast tego jest rysowana z dystrybucji beta ze średnią $ \ bar {p} = 1 / n $ i jakiś parametr kształtu $ \ nu $

$$ p \ sim Beta \ left (\ alpha = \ nu \ frac {1} {n}, \ beta = \ nu \ frac {n-1} {n } \ right) $$

Następnie liczba zdarzeń dla określonej kości $ n $ będzie rozdzielona dwumian beta. Prawdopodobieństwo wystąpienia 1 lub więcej zdarzeń będzie następujące:

$$ P (k \ geq 1) = 1 - \ frac {B (\ alpha, n + \ beta)} {B (\ alpha, \ beta)} = 1 - \ frac {B (\ nu \ frac {1} {n}, n + \ nu \ frac {n-1} {n})} {B (\ nu \ frac {1} {n}, n + \ nu \ frac {n-1} {n})} $$

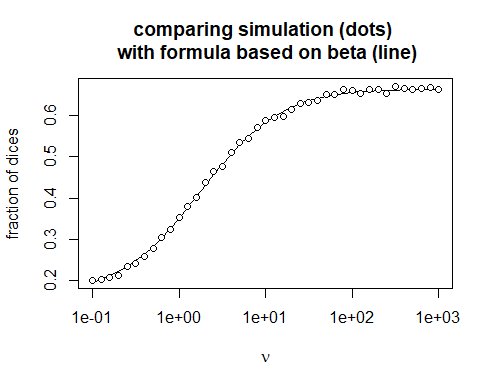
Mogę zweryfikować obliczeniowo, że to działa ...

  ### oblicz wynik rzutu n-stronną kostką n razy
rolldice <- function (n, nu) {
  p <- rbeta (1, nu * 1 / n, nu * (n-1) / n)
  k <- rbinom (1, n, p)
  out <- (k>0)
  na zewnątrz
}

### oblicz średnią dla próbki kości
meandice <- function (n, nu, reps = 10 ^ 4) {
  sum (replicate (reps, rolldice (n, nu))) / reps
}
meandice < - Vectorize ((meandice))
### symulacja i obliczanie wariancji n

set.seed (1)
n <- 6
nu <- 10 ^ seq (-1,3,0,1)
y <- meandice (n, nu)
plot (nu, 1-beta (nu * 1 / n, n + nu * (n-1) / n) / beta (nu * 1 / n, nu * (n-1) / n), log = "x ", xlab = wyrażenie (nu), ylab =" ułamek kości ",
     main = "porównanie symulacji (kropki) \ n ze wzorem opartym na beta (linia)", main.cex = 1, type = "l")
punkty (nu, y, lty = 1, pch = 21, col = "black", bg = "white")
 

.... Ale nie mam dobrego sposobu, aby analitycznie rozwiązać wyrażenie dla $ n \ to \ infty $ .

Wz czasem oczekiwania Jednak z czasami oczekiwania mogę wyrazić granicę rozkładu beta dwumianu (który jest teraz bardziej podobny do rozkładu beta Poissona) z wariancją wykładniczego współczynnika czasów oczekiwania.

Więc zamiast $ 1-e ^ {- 1} $ szukamy $$ 1- \ int e ^ {- \ lambda} p (\ lambda) \, \ text {d} \, \ lambda $$ .

Teraz ten człon całkowy jest powiązany z funkcją generującą moment (z $ t = -1 $ ). Więc jeśli $ \ lambda $ jest dystrybuowany normalnie z $ \ mu = 1 $ i variance $ \ sigma ^ 2 $ to powinniśmy użyć:

$$ 1-e ^ {- (1- \ sigma ^ 2/2)} \ quad \ text {zamiast} \ quad 1-e ^ {- 1} $$

Aplikacja

Te rzuty kostką to model zabawki. Wiele problemów z życia codziennego będzie miało zróżnicowanie i nie będzie do końca sprawiedliwych sytuacji na kościach.

Załóżmy na przykład, że chcesz zbadać prawdopodobieństwo, że dana osoba może zachorować na wirusa po pewnym czasie kontaktu. Można by oprzeć obliczenia w tym zakresie na podstawie pewnych eksperymentów, które weryfikują prawdopodobieństwo transmisji (np. Niektóre prace teoretyczne lub eksperymenty laboratoryjne mierzące / określające liczbę / częstotliwość transmisji w całej populacji w krótkim czasie), a następnie ekstrapolować tę transmisję na cały miesiąc. Powiedzmy, że okaże się, że transmisja wynosi 1 transmisję na miesiąc na osobę, a następnie można wywnioskować, że 1-1 USD / e \ około 0,63 \% $ populacji otrzyma chory. Jednak może to być przeszacowanie, ponieważ nie każdy może zachorować / zarazić się z taką samą częstością. Procent prawdopodobnie spadnie.

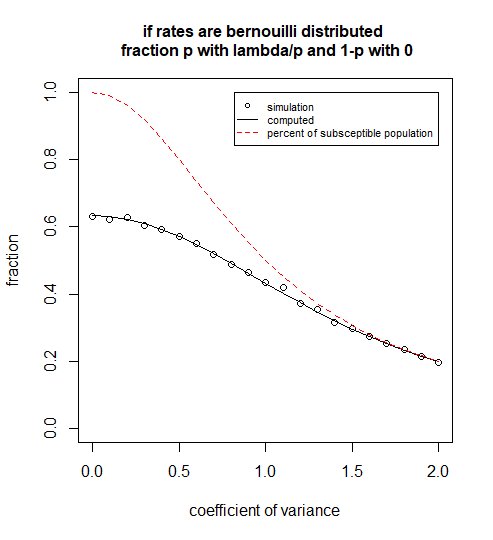
Jest to jednak prawdziwe tylko wtedy, gdy rozbieżność jest bardzo duża. W tym celu dystrybucja $ \ lambda $ musi być bardzo wypaczona. Ponieważ, chociaż wcześniej wyrażaliśmy to jako rozkład normalny, wartości ujemne nie są możliwe, a rozkłady bez rozkładów ujemnych zazwyczaj nie będą miały dużych współczynników $ \ sigma / \ mu $ , chyba że są mocno przekrzywione. Sytuację z dużym pochyleniem modeluje się poniżej:

Teraz używamy MGF dla rozkładu Bernoulliego (jego wykładnika), ponieważ modelowaliśmy rozkład jako $ \ lambda = 0 $ z prawdopodobieństwem $ 1-p $ lub $ \ lambda = 1 / p $ z prawdopodobieństwem $ p $ .

  set.seed (1)
stopa = 1
czas = 1
CV = 1
### oblicz wynik zachorowania ze zmienną częstością
getsick <- function (rate, CV = 0,1, time = 1) {
            ### obcinanie zmian sd i mean, ale nie za dużo, jeśli CV jest małe
  p <- 1 / (CV ^ 2 + 1)
  lambda <- rbinom (1,1, p) / (p) * stopa
  k <- rpois (1, lambda * czas)
out <- (k>0)
  na zewnątrz
}


CV <- seq (0,2,0.1)
plot (-1, -1, xlim = c (0,2), ylim = c (0,1), xlab = "współczynnik wariancji", ylab = "frakcja",
     cex.main = 1, main = "jeśli stawki są podzielone przez Bernouilli \ n ułamek p z lambda / p i 1-p z 0")
dla (CV w CV) {
  punkty (cv, suma (replicate (10 ^ 4, getsick (rate = 1, cv, time = 1))) / 10 ^ 4)
}

p <- 1 / (CV ^ 2 + 1)
wiersze (CV, 1- (1-p) -p * exp (-1 / p), col = 1)
linie (CV, p, col = 2, lty = 2)

legenda (2,1, c ("symulacja", "wyliczony", "procent subceptowalnej populacji"),
       col = c (1,1,2), lty = c (NA, 1,2), pch = c (1, NA, NA), xjust = 1, cex = 0,7)
 

Konsekwencja jest taka. Powiedzmy, że masz wysokie $ n $ i nie masz możliwości obserwowania $ n $ rzutu kośćmi (np. za długi), a zamiast tego sprawdzasz liczbę $ n $ rzuca się tylko przez krótki czas dla wielu różnych kości. Następnie możesz obliczyć liczbę kostek, które wyrzuciły liczbę $ n $ w tym krótkim czasie i na podstawie tego obliczenia, co stanie się dla $ n $ rolkach. Ale nie wiedziałbyś, jak bardzo wydarzenia są skorelowane w kostkach. Może się zdarzyć, że masz do czynienia z wysokim prawdopodobieństwem w małej grupie kości, zamiast równomiernie rozłożonego prawdopodobieństwa na wszystkie kości.

Ten „błąd” (lub można by rzec uproszczenie) odnosi się do sytuacji z COVID-19, gdzie pojawia się przekonanie, że potrzebujemy 60% osób odpornych, aby osiągnąć odporność stadną. Jednak może tak nie być. Obecny wskaźnik infekcji jest określany tylko dla niewielkiej grupy ludzi, może być tak, że jest to tylko wskazanie do zakaźności wśród niewielkiej grupy osób.

Uprość, a następnie rozszerz. Zacznij od monety. Moneta to kostka z 2 stronami (S = 2).

Wyczerpująca przestrzeń prawdopodobieństwa to

T | H

Dwie możliwości. Jeden spełnia stan wszystkich głów. Więc twoje szanse na wszystkie reszki z jedną monetą (n = 1) wynoszą 1/2.

Więc spróbuj dwóch monet (n = 2). Wszystkie wyniki:

TT | TH | HT | HH

Cztery możliwości. Tylko jeden spełnia Twoje kryteria. Warto zauważyć, że prawdopodobieństwo, że jedna będzie orłem, a druga reszką, wynosi 2/4, ponieważ dwie możliwości z czterech pasują do twoich kryteriów. Ale jest tylko jeden sposób, aby zdobyć wszystkie głowy.

Dodaj jeszcze jedną monetę (n = 3) ...

TTT | THT | HTT | HHT

TTH | THH | HTH | HHH

8 możliwości. Tylko jeden spełnia kryteria - czyli 1/8 szans wszystkich głów.

Wzorzec to (1 / S) ^ n lub (1/2) ^ 3.

Dla kości S = 6, a mamy ich 6

Prawdopodobieństwo uzyskania 6 w dowolnym rzucie wynosi 1/6. Rolls to niezależne wydarzenia. Zatem użycie 2 kostek do otrzymania wszystkich 6 to (1/6) * (1/6) lub 1/36.

(1/6) ^ 6 to około 1 na 46 656