Chociaż Henry dał już sposób na dokładne obliczenie liczby, zliczając wszystkie partycje, może być interesujące poznanie dwóch przybliżonych metod.
Ponadto istnieje alternatywne dokładne obliczenie oparte na warunkowych zmiennych rozproszonych Poissona.
Symulacja obliczeniowa
Nie będzie łatwo obliczyć wszystkich 12 $ ^ {18} $ możliwości (i nie będzie łatwo skalować problemu), ale możesz kazać komputerowi symulować losowo podzbiór możliwych sposobów i uzyskać rozkład z tych symulacji.
# funkcja do próbkowania 18 urodzeń
# i uzyskaj maksymalną liczbę podobnych miesięcy
monthample <- function () {
x <- sample (1: 12,18, zamień = TRUE) # sample
n <- max (tabela (x)) # uzyskaj maksimum
powrót (n)
}
# próbki milion razy
y <- replicate (10 ^ 6, monthample ())
# uzyskać częstotliwość za pomocą histogramu
h<-hist (y, breaks = seq (-0,5,18,5,1))
Aproksymacja za pomocą Poissonacji
Częstotliwość liczby urodzin w poszczególnych miesiącach to w przybliżeniu rozkład Poissona / dwumianowy. Na tej podstawie możemy obliczyć prawdopodobieństwo, że liczba urodzin w danym miesiącu nie przekroczy pewnej wartości, a biorąc potęgę dwunastu, obliczamy prawdopodobieństwo, że dzieje się to przez wszystkie dwanaście miesięcy.
Uwaga: tutaj pomijamy fakt, że liczba urodzin jest skorelowana, więc oczywiście nie jest to dokładne.
# przybliżenie z rozkładem Poissona
t <- 0:18
z <- ppois (t, 1,5) ^ 12 # P (max < = t)
dz <- diff (z) # P (max = t + 1)
Obliczenia z reprezentacją Bruce'a Levina
W komentarzach Whuber wskazał na pakiet pmultinom. Ten pakiet jest oparty na publikacji Bruce Levin 1981 „A Representation for Multinomial Cumulative Distribution Functions” w Ann. Statystyk. Tom 9 . Wynik miesięcy urodzenia (który jest dokładniej rozłożony zgodnie z rozkładem wielomianowym) jest reprezentowany jako niezależne zmienne o rozkładzie Poissona. Ale w przeciwieństwie do wcześniej wspomnianych naiwnych obliczeń, rozkład tych zmiennych o rozkładzie Poissona jest uważany za warunkowy , gdy całkowita suma jest równa $ n = 18 $ .
Więc powyżej obliczyliśmy $$ P (X_1, X_2, \ ldots, X_ {12} \ leq 4) = P (X_1 \ leq 4) \ cdot P (X_1 \ leq 4) \ cdot \ ldots \ cdot P (X_ {12} \ leq 4) $$ , ale powinniśmy obliczyć prawdopodobieństwo warunkowe dla wszystkich zmiennych rozłożonych Poissona równych lub mniejszych niż $$ P (X_1, X_2, \ ldots, X_ {12} \ leq 4 \ vert X_1 + X_2 + \ ldots + X_ {12} = 18) $$ , które wprowadza dodatkowy termin oparty na regule Bayesa.
$$ P (\ forall i: X_i \ leq 4 \ vert \ sum X_i = 18) = P (\ forall i: X_i \ leq 4) \ frac {P ( \ sum X_i = 18 \ vert \ forall i: X_i \ leq 4)} {P (\ sum X_i = 18)} $$
Ten współczynnik korygujący to stosunek prawdopodobieństwa, że suma obciętych zmiennych o rozkładzie Poissona będzie równa 18 $ P (\ sum X_i = 18 \ vert \ forall i: X_i \ leq 4 ) $ , a prawdopodobieństwo, że suma zwykłych zmiennych o rozkładzie Poissona jest równa 18, $ P (\ sum X_i = 18) $ . W przypadku małej liczby miesięcy urodzenia i osób w grupie ten skrócony rozkład można obliczyć ręcznie
# współczynnik korekty autorstwa Bruce'a Levina
korekta <- function (y) {
Nptrunc (y) [19] / dpois (18,18)
}
Funkcja Nptrunc < (lim) {
# obcięty rozkład Poissona
ptrunc <- dpois (0: lim, 1,5) / sum (dpois (0: lim, 1,5))
## wektor z prawdopodobieństwami
outvec <- rep (0, lim * 12 + 1)
outvec [1] <- 1
# konwój 12 razy w każdym miesiącu
for (i in 1:12) {
newvec <- rep (0, lim * 12 + 1)
for (k in 1: (lim + 1)) {
newvec <- newvec + ptrunc [k] * c (rep (0, k-1), outvec [1: (lim * 12 + 1- (k-1))])
}
outvec <- newvec
}
outvec
}
z2 <- ppois (t, 1,5) ^ 12 * Wektoryzacja (korekta) (t) # P (max< = t)
z2 [1: 2] <- c (0,0)
dz2 <- diff (z2) # P (max = t + 1)
Wyniki
Te przybliżenia dają następujące wyniki
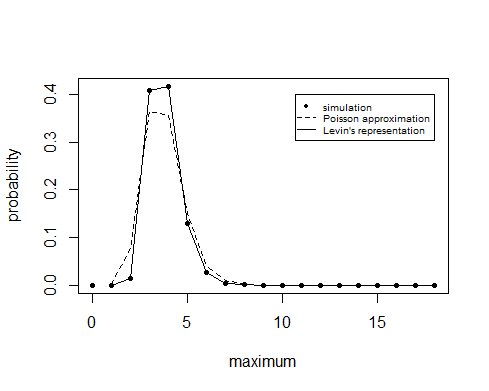
> ### symulacja
Suma > (y> = 4) / 10 ^ 6
[1] 0,577536
Obliczenia > ###
> 1-z [4]
[1] 0,5572514
> ### obliczenie dokładne
> 1-z2 [4]
[1] 0,5771871